选择行，

选择列

选择行列

hist 直方图

from matplotlib import pyplot as plt

from matplotlib import font_manager

a=[zifuchuan]

plot.hist(a.fenzushu)

细节

计算组数=num_bin= (max(a)-nim(b)//d)

d=5

组数= 极差/组距

x轴的刻度设置

plt.xticks(range(min(a),max(a)+d,d))

plt.show()

图形大小：plt.figure(figsze=(20,8),dpi=80)

{数据}

数组的形状

shape即可查看数组的各个维度长度（输出按三维二维依次降低，块、行、个）

reshape方法可以重新设置行列，是有返回值的，而不改变本身

有返回值才会输出

结合shape和reshape可以做到在不清楚维度长度的情况下降维

flatten可以将数组展开变成一维

数组的计算

numpy数组对数字进行+*-/计算，是对全部单元进行计算

nan>>not a number 0/0

inf>>infinite x/0

数组对数组进行计算：

不同维度的数组进行计算至少有一个维度的长度相同

广播会在缺失或者长度为1的维度上进行（不同维度的计算本质上是广播）

广播原则：如果两个数组的后缘维度，即从末尾开始算起的维度轴长相符，或者某一方的长度为1，即广播jian'r

一维数组只有0轴，二维有0、1轴，三维有0、1、2轴

reshape(0,1,2)，shape输出(2,1,0)

CSV逗号分隔值文件

numpy的读取文件方法

unpack参数实现行列转置

transpose,T,swapaxes(1,0)方法实现行列转置

numpy的索引和切片

索引从0开始

2:取得连续多行，[[2,5,6]]多一个[]取得不连续的行

:,1取得单列

:,1:取得连续列

:,[]取得不连续列

取得行列交叉的内容

取得不相邻的点

这个老师的逻辑能力和语言组织能力真的是匮乏 前言不搭后语 自己把自己绕进去了

讲的真垃圾

这课程讲的就和拿着稿子照本宣科一样

提升：

梯度提升

Gradient Descent

Gradient：loss损失函数等高线的发现方向

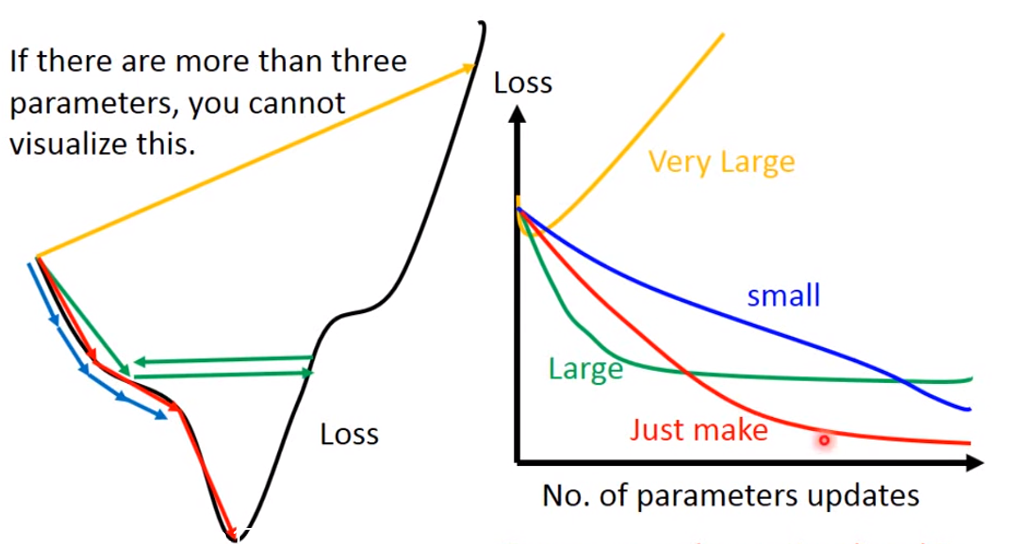
需要注意的是：learning rate 需要设置合理

如果learning rate很小，loss下降的很慢；

如果learning rate表达大，可能卡住，找不到loss的极小值；

如果learning rate非常大，loss有可能越来越大

只有当learning rate 刚刚好的时候，我们才能得到loss的极小值

Adagrad

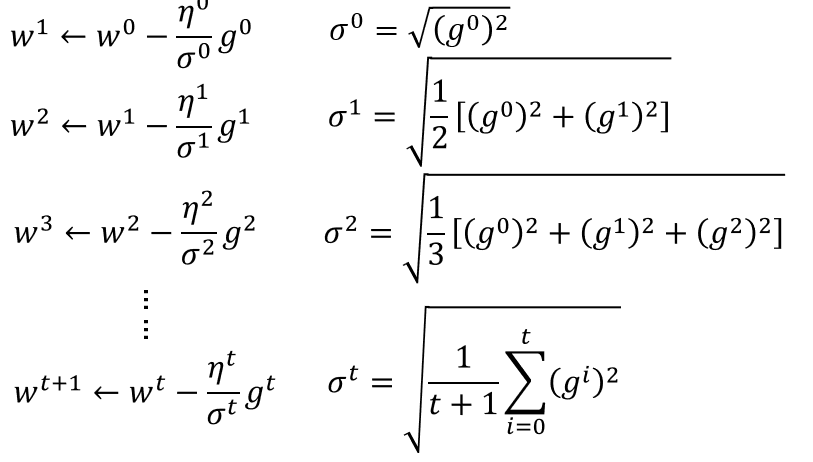
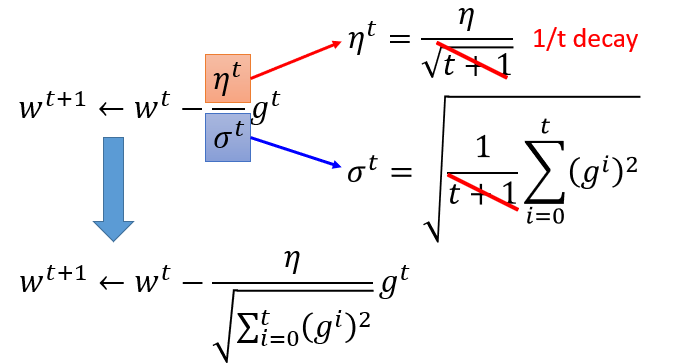
有个矛盾点是，对于gt来说，梯度越大，w参数应该下降得越快，但是分母上也有g的和，分母越大，w参数值下降得越小，这里应该如何理解？

对于2次函数来说，可以直观的看出Adagrad的优势

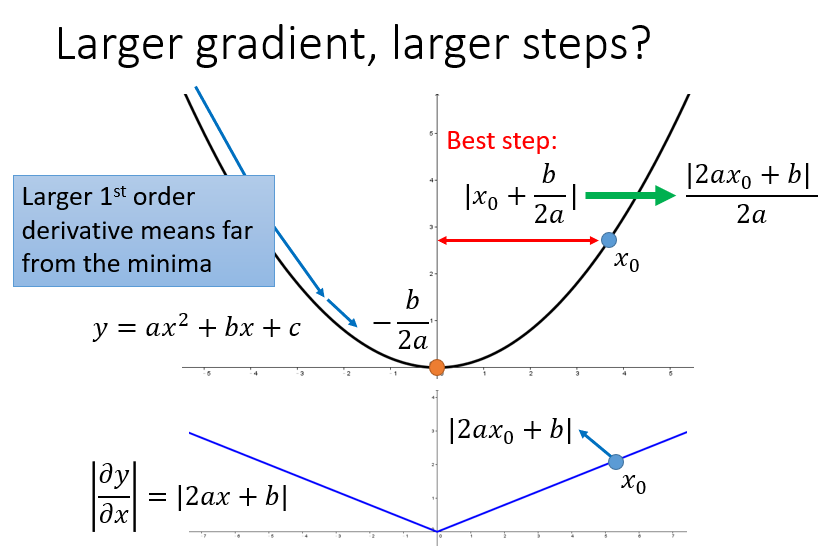
最好的步长是一阶导的绝对值除以二阶导的值

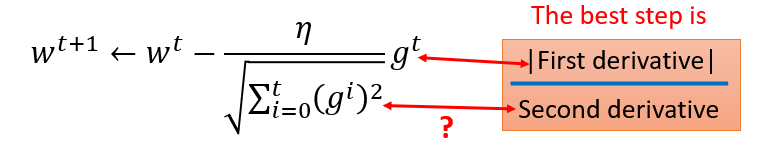
这里的分母虽然是一阶导的绝对值的和，但在一定程度上可以看出二阶导的大小来

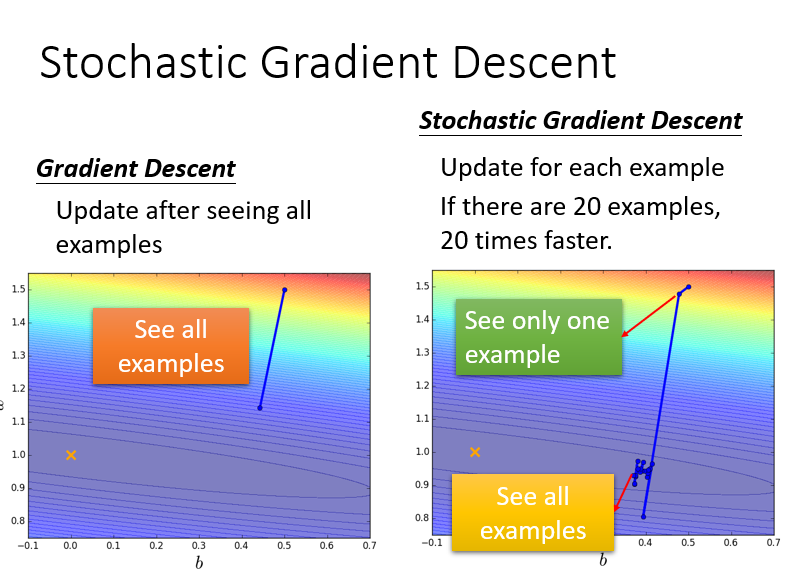
Stochastic Gradient Descent

只看一个example，只考虑一个点的参数值（其实没听懂）

Feature Scaling

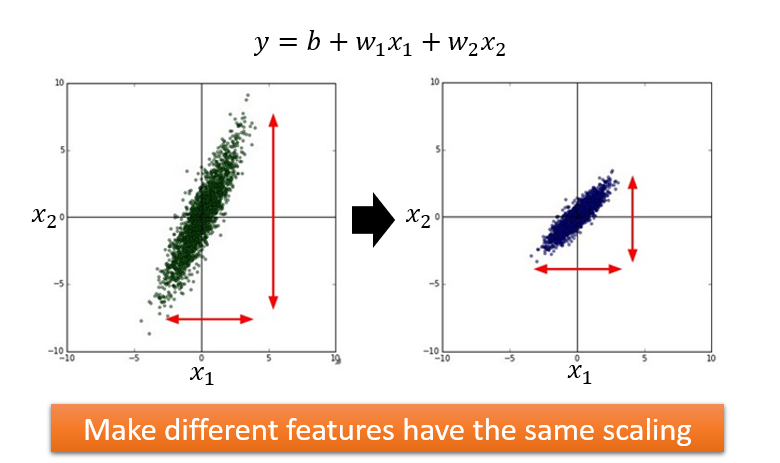
做法：

梯度下降背后的数学原理

泰勒定理：

多元的情况下：

误差来源于两个——一个是bias，还有一个是variance。出现bias是由于开始就没有瞄准靶心；出现vaiance是由于瞄准了靶心，但是发射的时候出现了偏离。我们的目标是低bias和低variance。

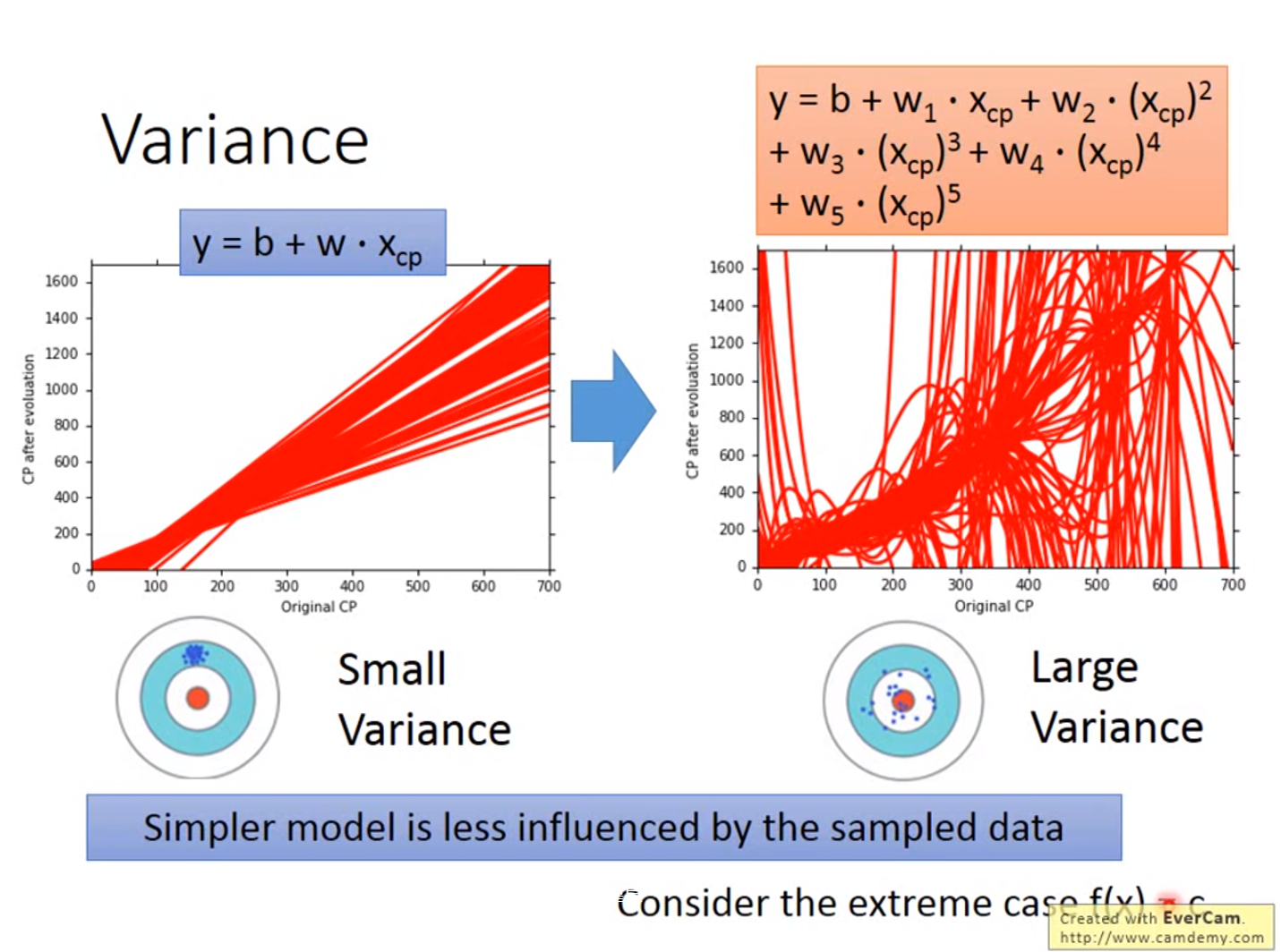
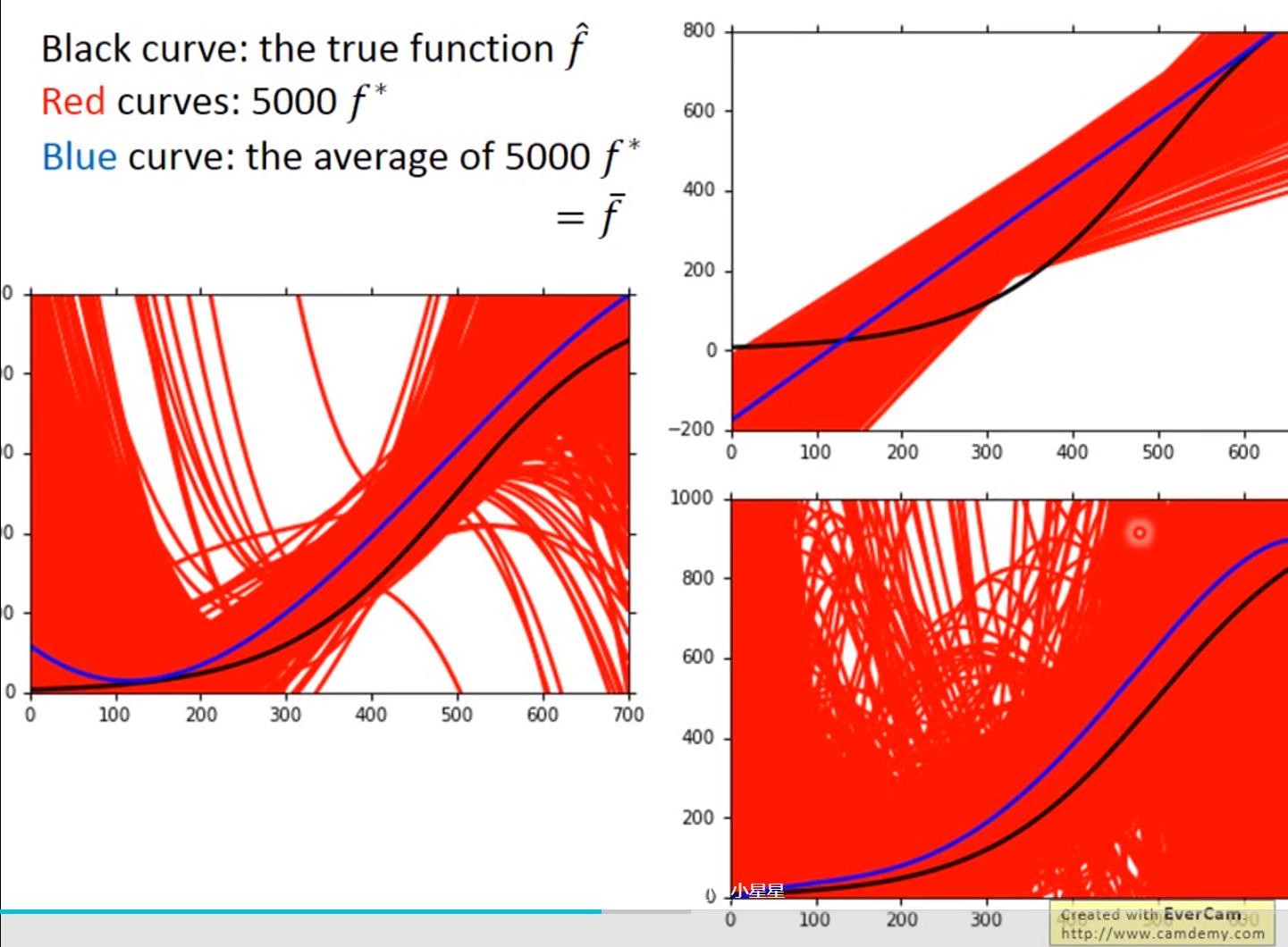
红色的部分是分别在考虑输入值一次方、三次方和五次方函数进行5000次实验的结果，蓝色的线条是将5000次实验结果进行平均即结果

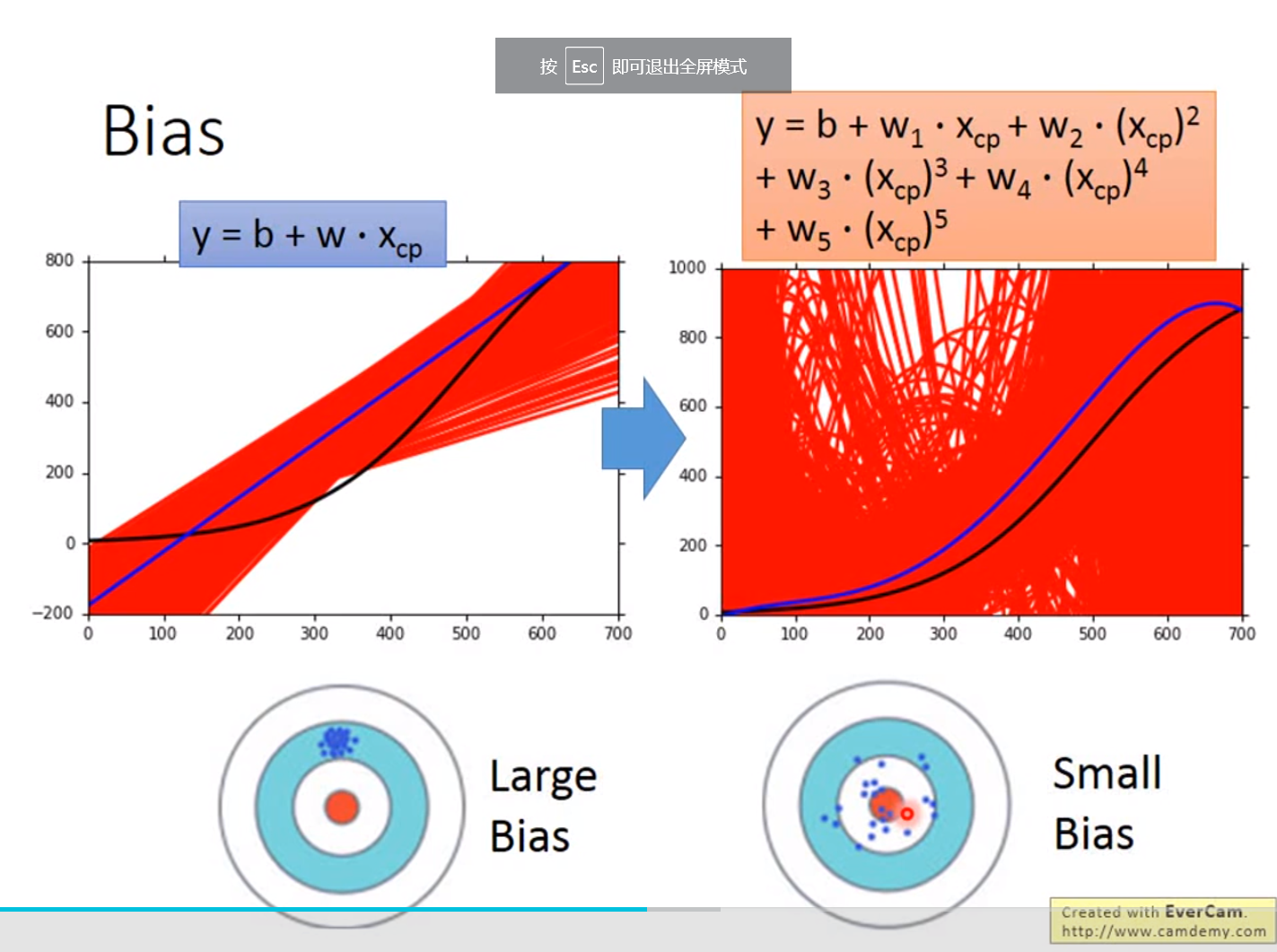
越简单的模型，bias越大，variance比较小；反之，模型越复杂，variance越大，但是平均值却比较接近于期望值

bias较大的情况，问题出现在underfitting；

variance较大的情况，问题出现在overfitting

Diagnosis：

(1)当模型不能拟合训练集时，我们有较大的bias；

(2)当模型可以集合训练集，但是在测试集上出现了较大的损失值，则很大可能上有较大的variance

for bias, redesign模型：
（1）add more feature as input

（2）a more complex model

for variance

（1）more data（增加每次实验的样本量）

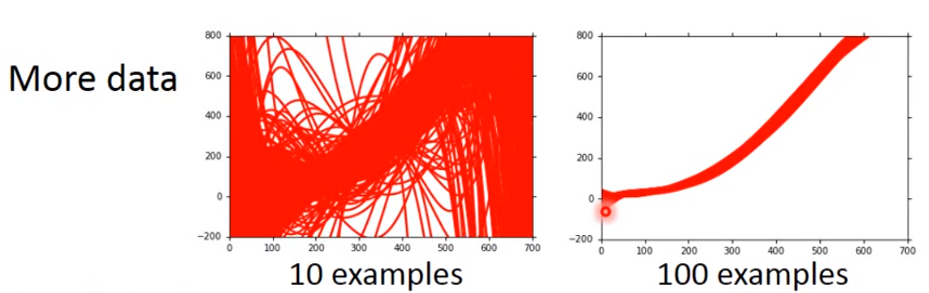
（2）Regularization我们希望曲线越平缓越好

伤害：只包含了比较平滑的曲线，在取值上产生了较大的bias

model selection：

我们想要找到尽可能小的bias和variance来得到最小的损失值

Regression回归

1、应用场景

（1）Stock Market Forecast

（2）Self-driving Car

（3）Recommendation

2、步骤

（1）给一个Model

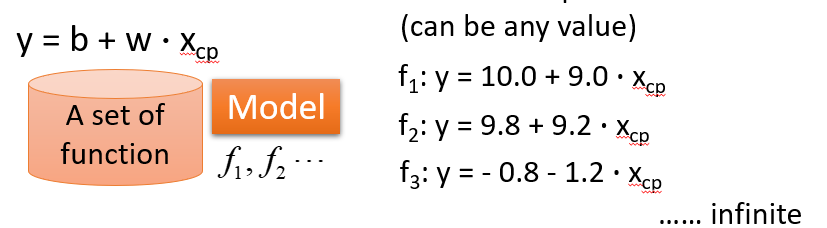
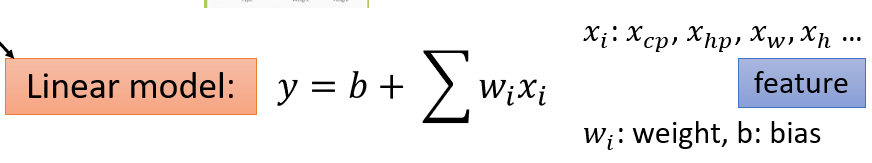
（2）Goodness of Function（函数优度）

输入：a function一个函数

输出：loss funchtion——how bad it is 

Pick the “Best”Function

（3）Gradient Descent

梯度下降：初试化w和b这两个参数，不断迭代更新，知道找到最优解，也就是使损失值达到最小的参数值

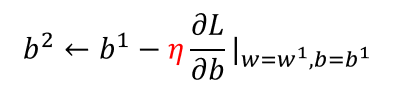
在线性回归里，是不需要担心找不到全局最优解的，因为其三维图形是一圈一圈的等高线，不管从哪个方向都可以找到最优解

how's the results？

训练的目的是损失值最小，但是通过训练集得到的损失值是比测试集得到的损失值小的，为了减少误差，我们需要改进模型——引入了二次方、三侧方和四次方的函数

overfitting——更复杂的模型会得到更不好的结果，所以模型并不是越复杂越好。

what are the hidden factors——pokemon的物种会影响他们值

根据不同的输入值，对不同的物种设置不同 的权重，此时仅设置了输入值的一次方，还可以考虑输入值的二次方函数

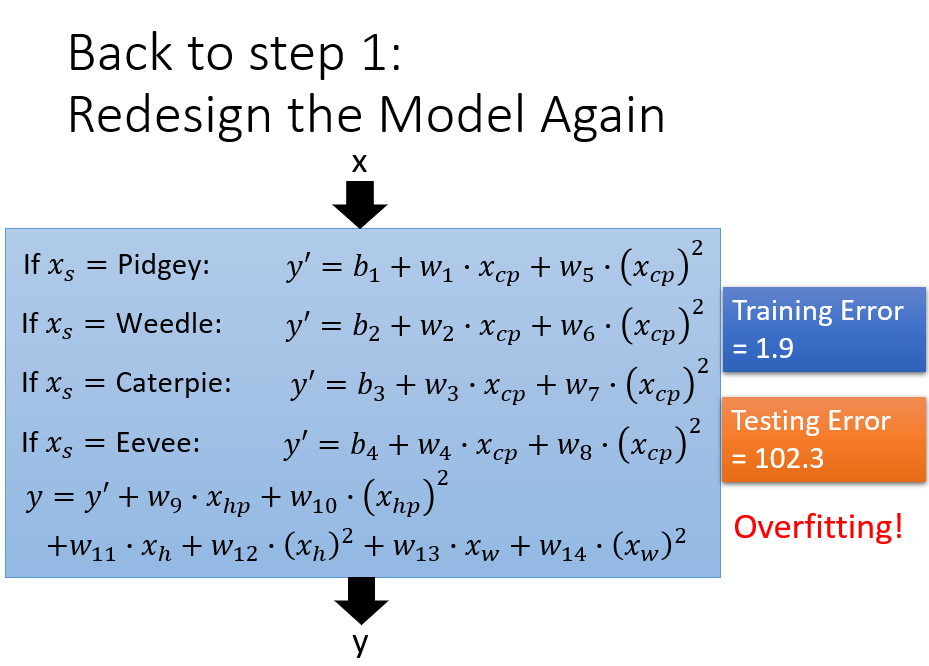
产生了过拟合的结果

设置较为平缓的曲线，由于w的值大于零小于1，当其越接近于0，结果是越为平缓的，前面的系数越大，代表我们越考虑smooth，越可以较多得关注参数w本身的值

连续[2:5,1:4]跳跃[[2,1],[3,5]]

SST (总方差)= SSE() + SSR （残差平方和）

只有无偏估计下成立，否则 SST≥SSE+ SSR

局部加权

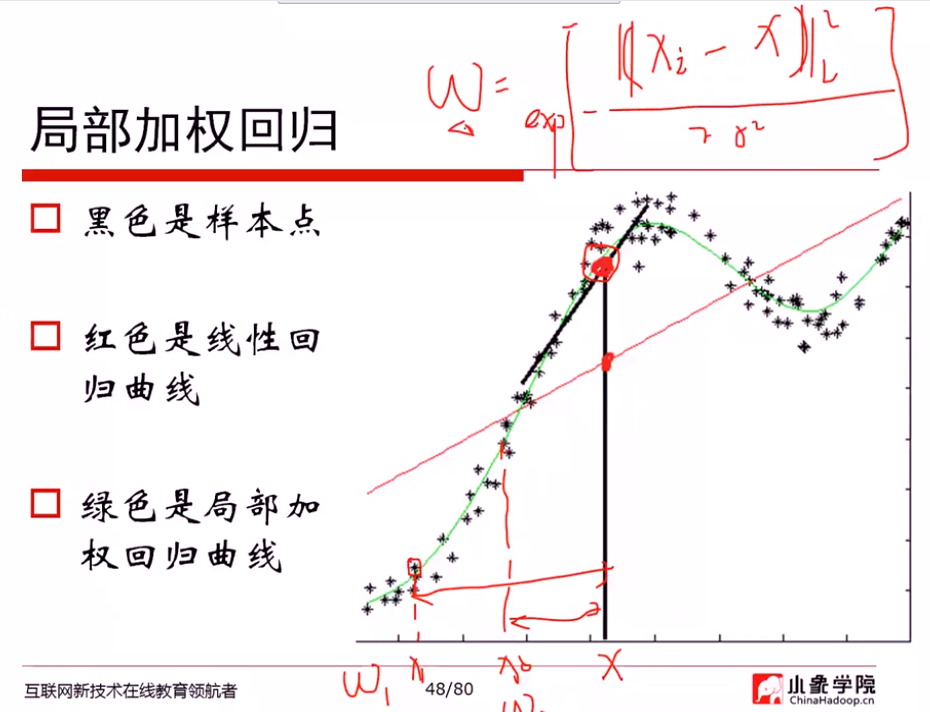
最重要的问题: 如何度量权重

Logistic回归

p(y|x:θ)  y=0, y=1时,写成上述密度函数形式

解法1: 从mle求解

极大似然估计的梯度上升算法，本质与梯度下降无区别，梯度上升取正梯度方向，同样设置步长a；梯度下降选取负梯度方向，

线性回归:  假定服从高斯分布，通过MLE进行估计

logistics回归: 假定服从二项分布，通过MLE进行估计

如果都进行梯度下降法估计，会发现求解的方式都是一样的

广义线性模型的定义: 因变量不服从正态分布，且因变量与自变量不存在线性关系；广义就是要找一个非线性的关系f，使得转换后更接近因变量的分布

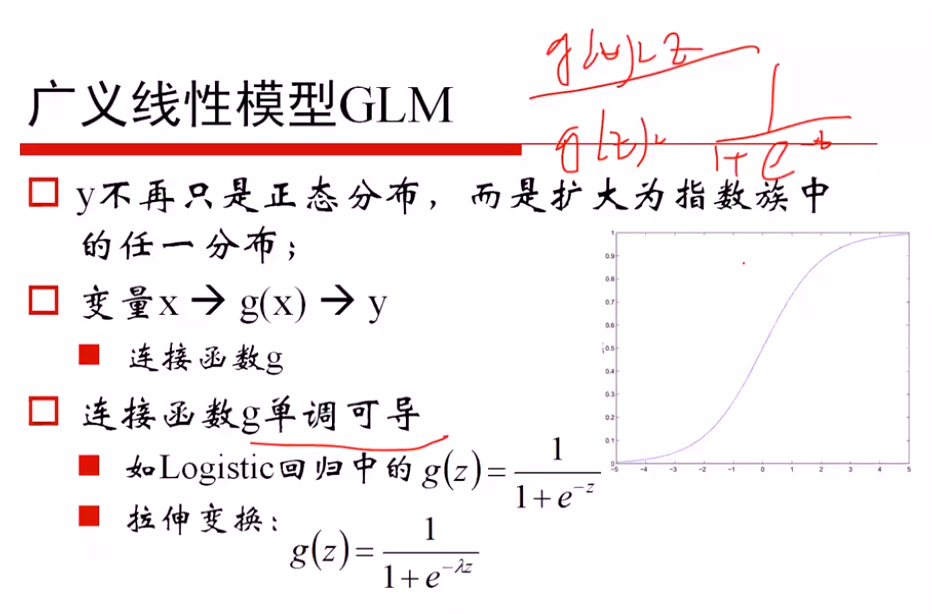
证明是一个广义的线性模型:

对数线性模型:

从对数模型理解 logistics函数

一方面: 从 ln(p/(1-p)) = θx 推导出 p = logistics函数，说明希望对数模型是线性的，从而推导出概率可以用logistics函数表示

另一方面: 从 p=logistics函数 + ln(p/(1-p))对数模型，推导出对数模型是线性的θTx

广义线性模型  → 相似的梯度下降方法

解法2: 从损失函数进行求解

(1)对 -1, 1转换为0, 1  进行(yi+1)/2...

softmax回归

鸢尾花数据

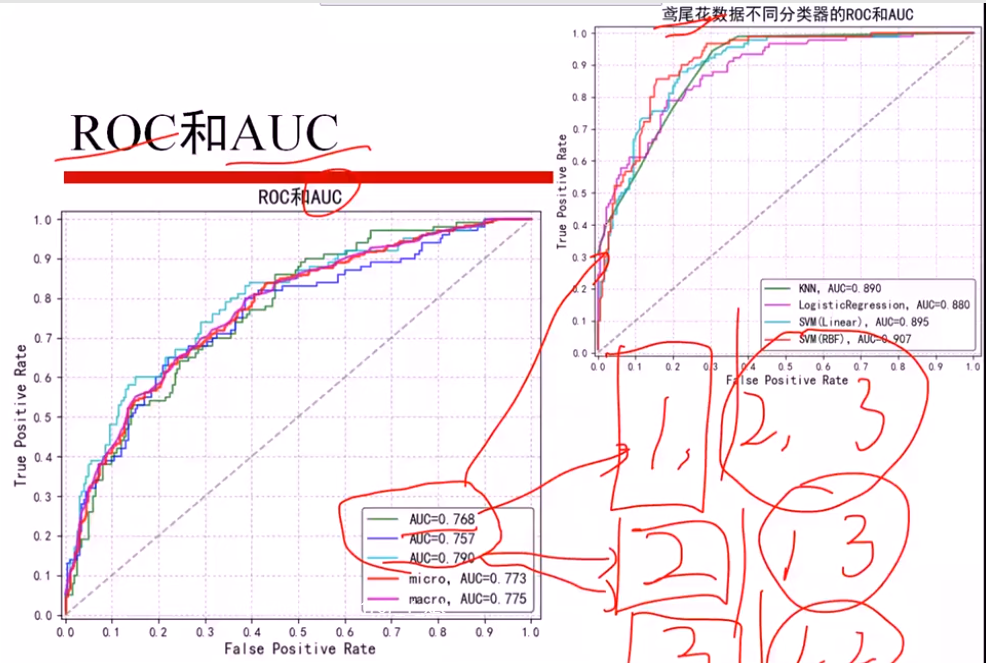
分为三个 二分类问题，算出三个AUCi值

micro: 直接算三个平均AUCi，得出AUC

macro: 总体加和，当作一个AUC计算

1. 线性回归

• 极大似然估计解释最小二乘

假设: 误差ξ服从高斯分布(0, δ)

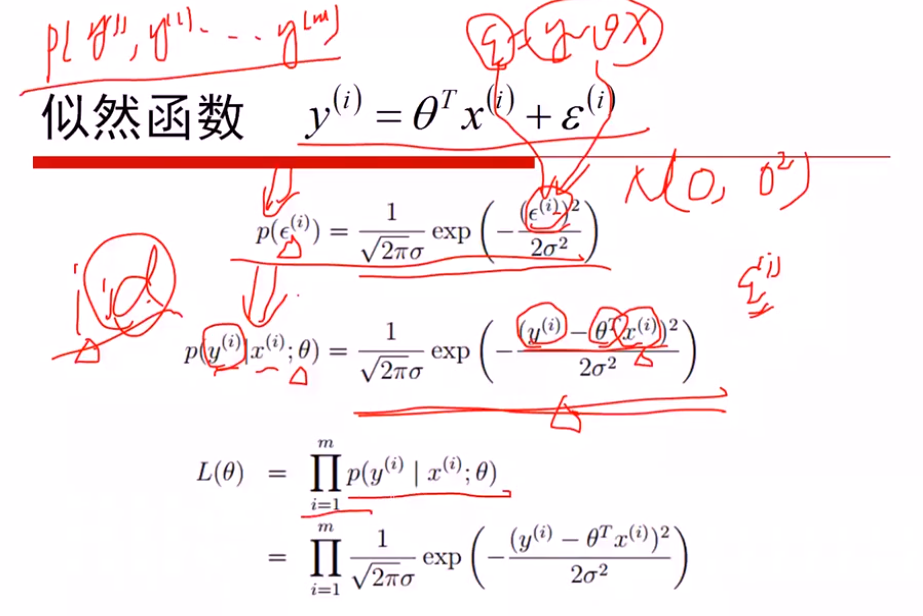
①最大化似然函数，对l(θ)进行简化

max l(θ)  等价于 min(J(θ))

• 1 最小二乘的矩阵推导

注意:

(1)是关于θ的函数，最大化θ参数

(2)J(θ)是一个xTx的凸函数，因为xTx是半正定的，开口向上，xTxθTθ就是关于θ的开口向上的二次函数

• 线性回归复杂度惩罚因子

（1）L2正则，进行对θ惩罚 -- Ridge回归

         L1正则，  --  Lasso回归

• 解释为什么L1有特征选择能力:

1 拉格朗日角度进行解释

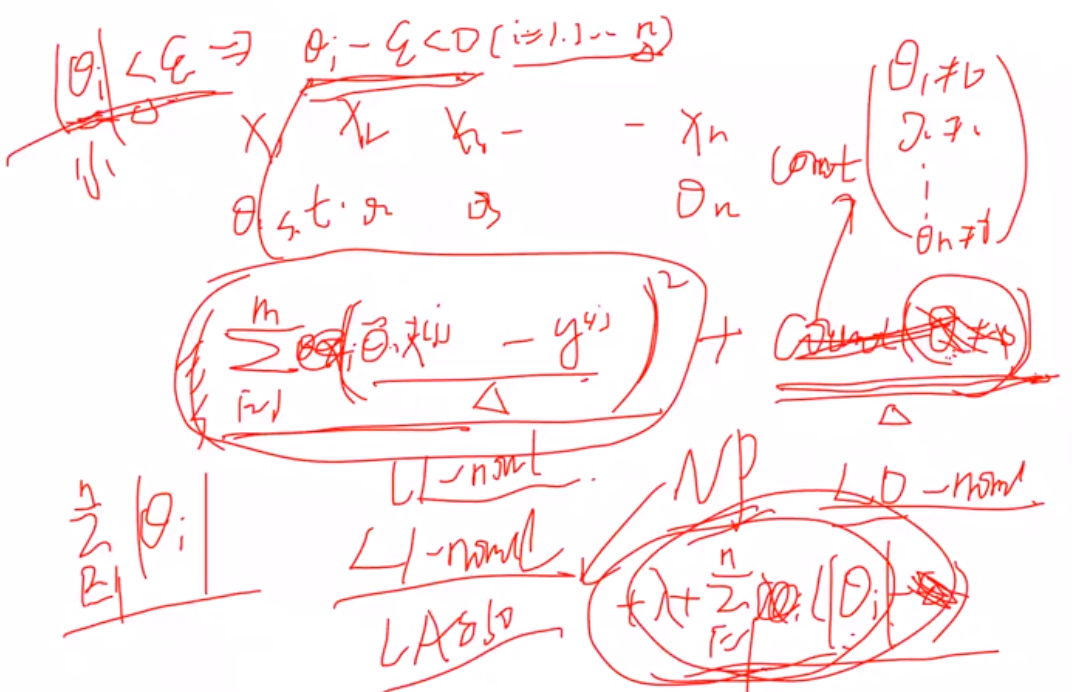
（1） 原本的目标: 希望θ=0就计0，不等于0就计为1，惩罚θ>0时候的数目，但是由于是无解的，因此用L1范数进行近似

推导看手稿:

2 几何解释:

L1约束使得某一个wi是0，稀疏约束

L2使得两个wi都比较小，约束

• L1正则不可导如何解决?

(1)坐标轴下降法

(2)近端梯度近似法...  其余还有很多

• 2 广义逆矩阵求解（伪逆）

（1）当x可逆， θx =y可以直接进行求解，不用进行目标函数最小化求解，因此可以利用SVD进行奇异值分解，求出伪逆矩阵后进行求解 

• 3 梯度下降法求解

1. Logistics 回归
2. 多分类softmax回归
3. 技术:

• 梯度下降
• 最大似然估计
• 特征选择

1. 1 贝叶斯, MLE的思想

假设1：p(Ai) 概率相似

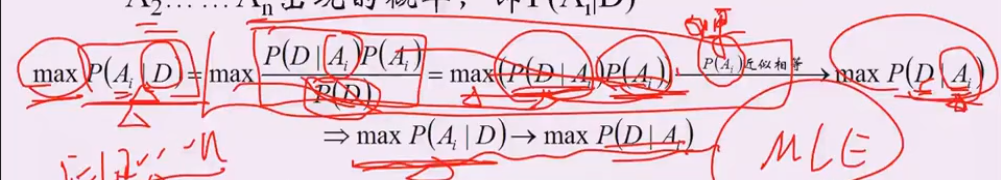
P（D|Ai)： 给定结论Ai下， 这个数据以多大的概率产生。 可以理解为x1..xn是未知的数据参数，θi是已知的参数，能够使  p(x1..xn|θi)最大的参数θi，就是我们想要估计的参数， 这里xi对应D，Ai对应参数θ

1. 2 赔率分析

公平赔率； y = 1/p   y是赔率，p是赢的概率

赔率公式    y =a/p

计算庄家盈亏:

10.5% = 0.21 a / 2a

1. 3 模糊查询与替换

2 PCA

2.1 原理

①求协方差矩阵

② 特征值排序

③ 方差最大的就认为是主要的方向，其中特征向量相互垂直，每一个特征向量就是一个方向，Aμi的方差最大，就认为是最主要的投影方向

①假定样本已经作了中心化，所以忽略均值E

Q 为什么特征值最大 等价于 求方差最大？

PCA中希望投影的方差最大，认为得到的信息最多。

目标函数: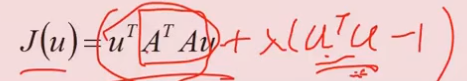

加上等式约束  μTμ=1， 根据拉格朗日求解，

aJ/aμ = 2ATAμ +2λμ = 0 ,求得λ就是 ATA的特征值。

因此，方差最大 等价于 最大特征值

2.2 过拟合问题

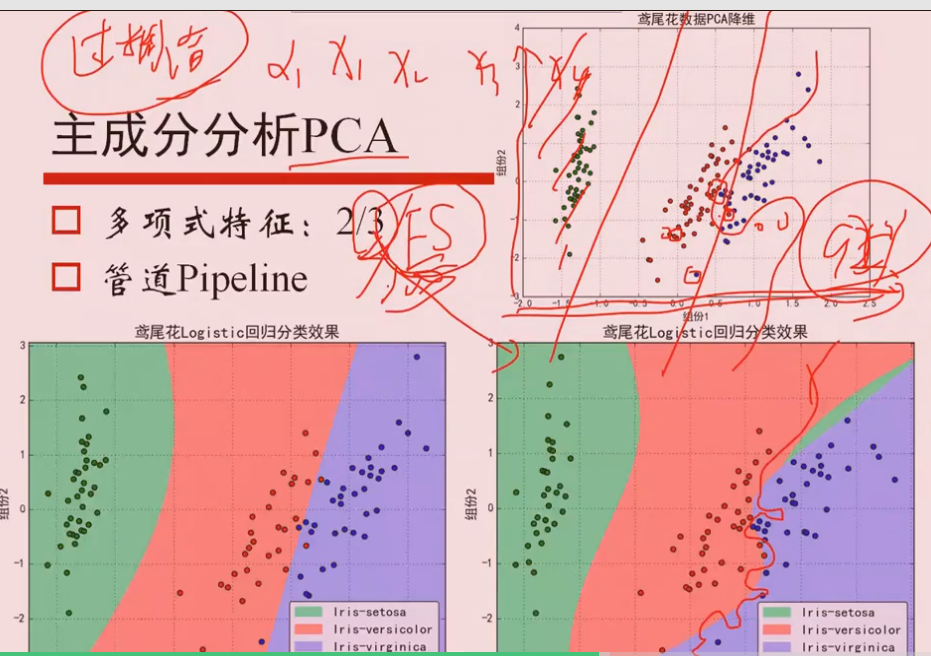
使用高阶的特征x1^2, x2^2...，特征过多，虽然会得到弯曲的曲线进行分离，但是很有可能产生过拟合问题

决策树不需要做one-hot编码

6.1 Prime

计算素数:  

fliter(函数, x): 把数字放入x中，结果输出

数据分析的流程:

1. 提出问题
2. 准备数据
3. 分析数据
4. 获得结论
5. 成果可视化

### 对于LightGBM：又轻又快

在不降低准确率的前提下，速度提升了10倍左右，占用内存下降了3倍左右。因为它是基于决策树算法的，它采用最优的==叶明智==策略分裂叶子节点，然而它的提升算法分裂树一般采用的是深度方向或者水平明智。因此，当增长到相同的叶子节点，叶明智算法比水平-wise算法减少更多得损失。因此导致更高的精度。