连续[2:5,1:4]跳跃[[2,1],[3,5]]

SST (总方差)= SSE() + SSR （残差平方和）

只有无偏估计下成立，否则 SST≥SSE+ SSR

局部加权

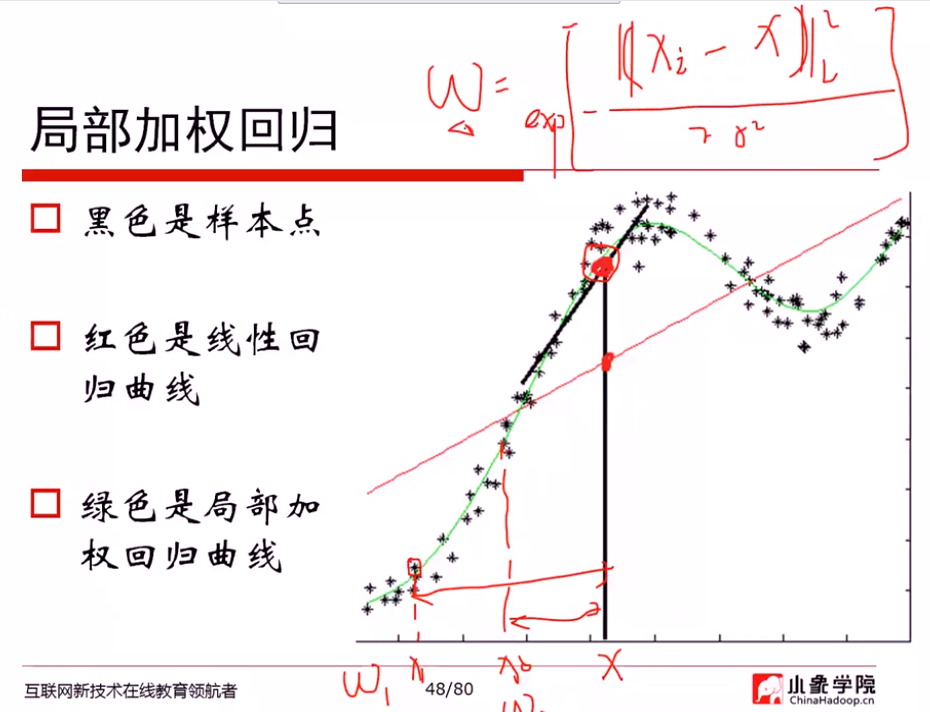
最重要的问题: 如何度量权重

Logistic回归

p(y|x:θ)  y=0, y=1时,写成上述密度函数形式

解法1: 从mle求解

极大似然估计的梯度上升算法，本质与梯度下降无区别，梯度上升取正梯度方向，同样设置步长a；梯度下降选取负梯度方向，

线性回归:  假定服从高斯分布，通过MLE进行估计

logistics回归: 假定服从二项分布，通过MLE进行估计

如果都进行梯度下降法估计，会发现求解的方式都是一样的

广义线性模型的定义: 因变量不服从正态分布，且因变量与自变量不存在线性关系；广义就是要找一个非线性的关系f，使得转换后更接近因变量的分布

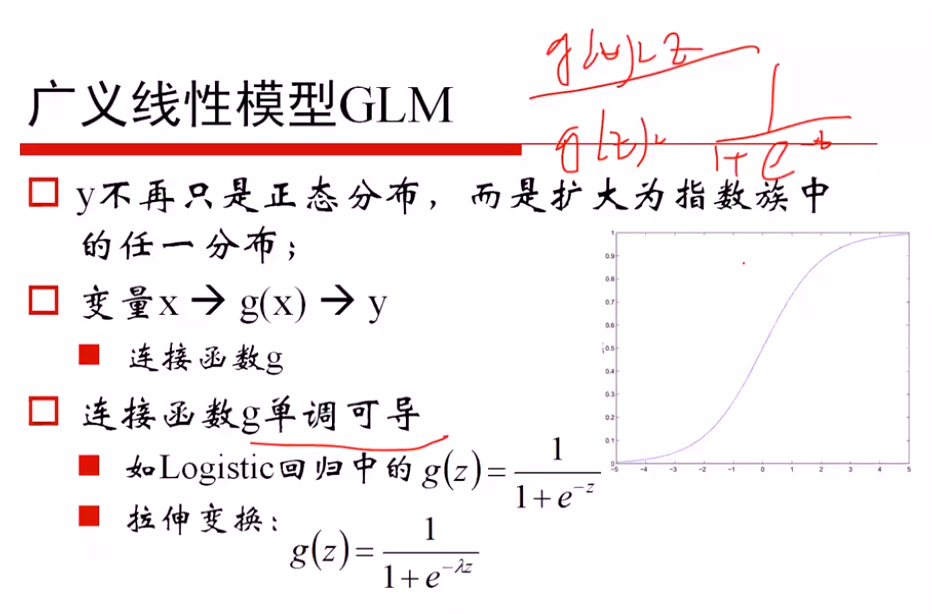
证明是一个广义的线性模型:

对数线性模型:

从对数模型理解 logistics函数

一方面: 从 ln(p/(1-p)) = θx 推导出 p = logistics函数，说明希望对数模型是线性的，从而推导出概率可以用logistics函数表示

另一方面: 从 p=logistics函数 + ln(p/(1-p))对数模型，推导出对数模型是线性的θTx

广义线性模型  → 相似的梯度下降方法

解法2: 从损失函数进行求解

(1)对 -1, 1转换为0, 1  进行(yi+1)/2...

softmax回归

鸢尾花数据

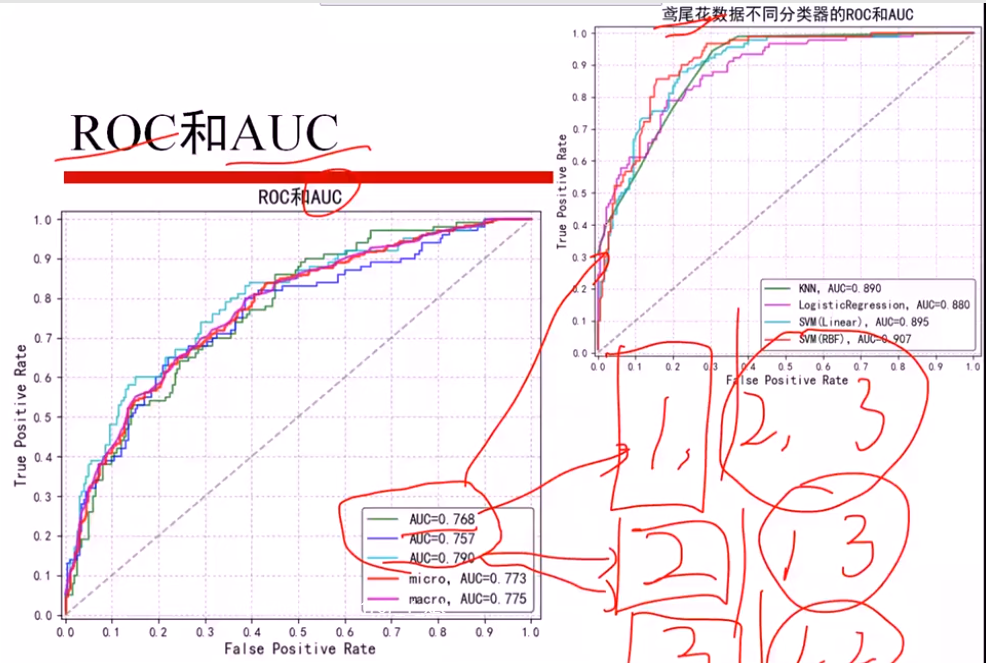
分为三个 二分类问题，算出三个AUCi值

micro: 直接算三个平均AUCi，得出AUC

macro: 总体加和，当作一个AUC计算

1. 线性回归

• 极大似然估计解释最小二乘

假设: 误差ξ服从高斯分布(0, δ)

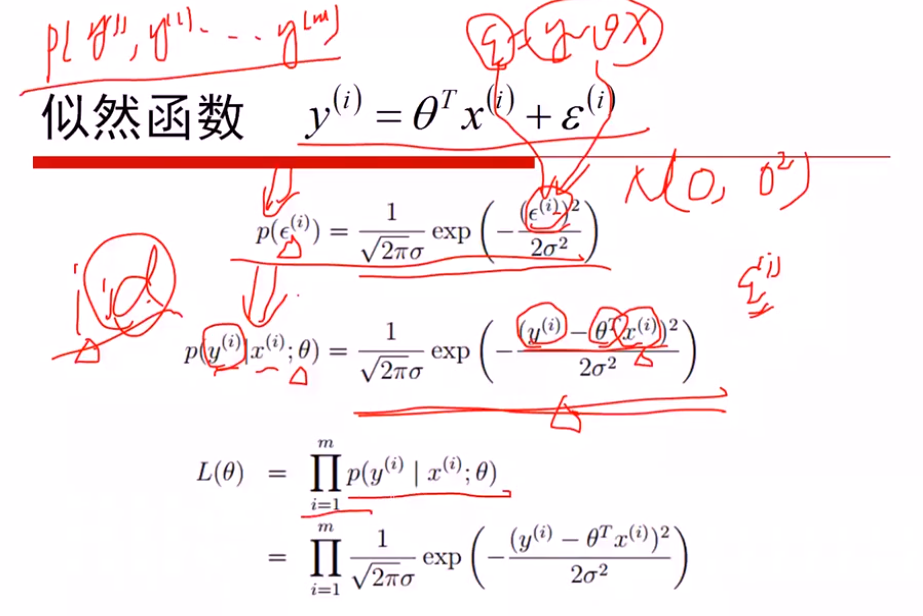
①最大化似然函数，对l(θ)进行简化

max l(θ)  等价于 min(J(θ))

• 1 最小二乘的矩阵推导

注意:

(1)是关于θ的函数，最大化θ参数

(2)J(θ)是一个xTx的凸函数，因为xTx是半正定的，开口向上，xTxθTθ就是关于θ的开口向上的二次函数

• 线性回归复杂度惩罚因子

（1）L2正则，进行对θ惩罚 -- Ridge回归

         L1正则，  --  Lasso回归

• 解释为什么L1有特征选择能力:

1 拉格朗日角度进行解释

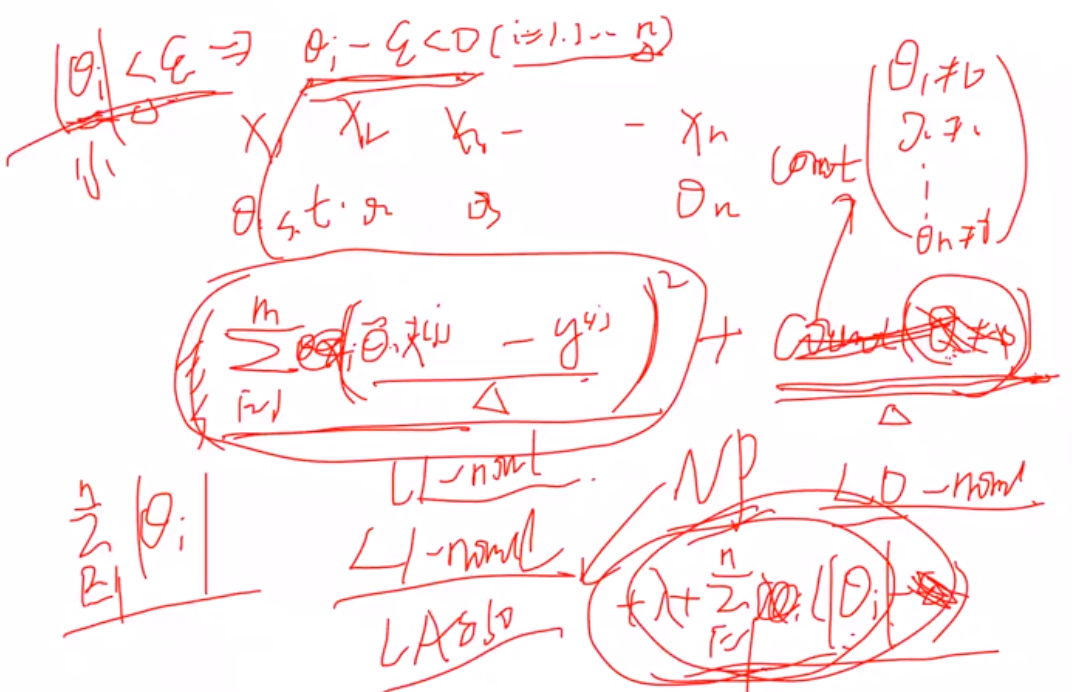
（1） 原本的目标: 希望θ=0就计0，不等于0就计为1，惩罚θ>0时候的数目，但是由于是无解的，因此用L1范数进行近似

推导看手稿:

2 几何解释:

L1约束使得某一个wi是0，稀疏约束

L2使得两个wi都比较小，约束

• L1正则不可导如何解决?

(1)坐标轴下降法

(2)近端梯度近似法...  其余还有很多

• 2 广义逆矩阵求解（伪逆）

（1）当x可逆， θx =y可以直接进行求解，不用进行目标函数最小化求解，因此可以利用SVD进行奇异值分解，求出伪逆矩阵后进行求解 

• 3 梯度下降法求解

1. Logistics 回归
2. 多分类softmax回归
3. 技术:

• 梯度下降
• 最大似然估计
• 特征选择

1. 1 贝叶斯, MLE的思想

假设1：p(Ai) 概率相似

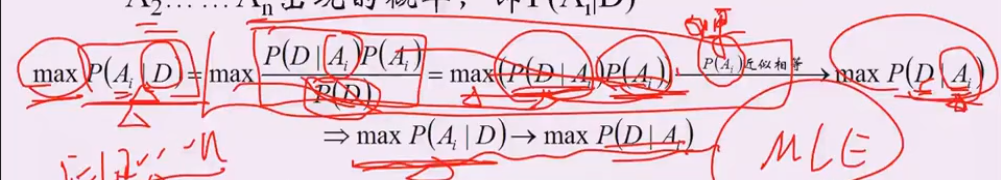
P（D|Ai)： 给定结论Ai下， 这个数据以多大的概率产生。 可以理解为x1..xn是未知的数据参数，θi是已知的参数，能够使  p(x1..xn|θi)最大的参数θi，就是我们想要估计的参数， 这里xi对应D，Ai对应参数θ

1. 2 赔率分析

公平赔率； y = 1/p   y是赔率，p是赢的概率

赔率公式    y =a/p

计算庄家盈亏:

10.5% = 0.21 a / 2a

1. 3 模糊查询与替换

2 PCA

2.1 原理

①求协方差矩阵

② 特征值排序

③ 方差最大的就认为是主要的方向，其中特征向量相互垂直，每一个特征向量就是一个方向，Aμi的方差最大，就认为是最主要的投影方向

①假定样本已经作了中心化，所以忽略均值E

Q 为什么特征值最大 等价于 求方差最大？

PCA中希望投影的方差最大，认为得到的信息最多。

目标函数: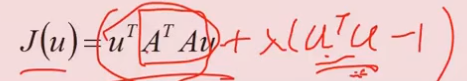

加上等式约束  μTμ=1， 根据拉格朗日求解，

aJ/aμ = 2ATAμ +2λμ = 0 ,求得λ就是 ATA的特征值。

因此，方差最大 等价于 最大特征值

2.2 过拟合问题

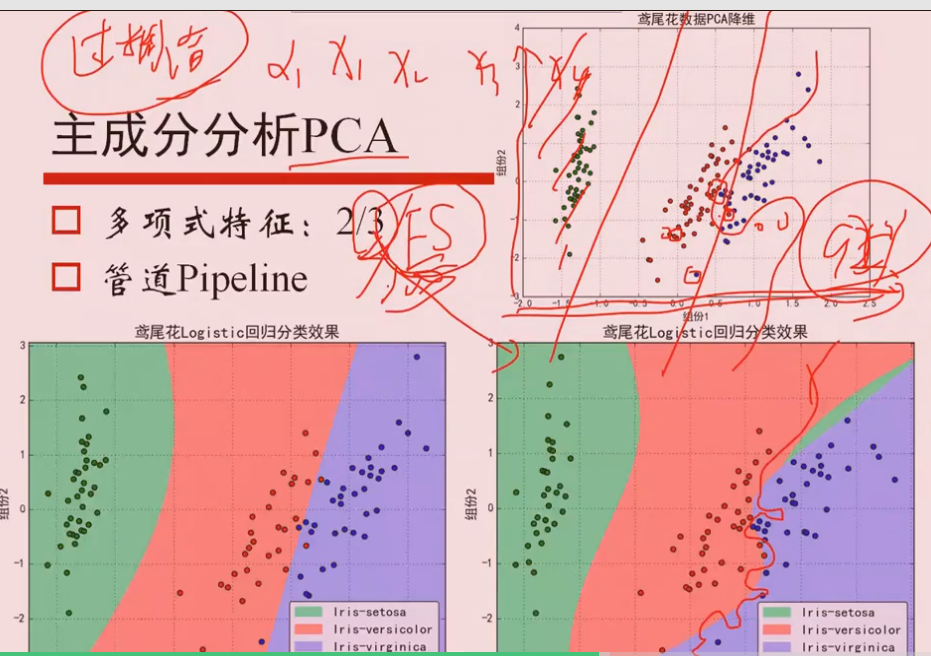
使用高阶的特征x1^2, x2^2...，特征过多，虽然会得到弯曲的曲线进行分离，但是很有可能产生过拟合问题

决策树不需要做one-hot编码

6.1 Prime

计算素数:  

fliter(函数, x): 把数字放入x中，结果输出

模型选择：了解每个模型；

EM算法无监督聚类燕尾花

GMM与图片分析

图像卷积

crawler 爬数据

1. 集合
2. 元素
3. 描述方式
4. ​​​​​​​子集
5.  

让机器学习程序替换手动步骤，减少企业的成本，也提高企业的效率

真是听过讲的最烂的，重点yong'yuan'tiao'guo

# Machine learning

- make decisions

- go right/left 

- increse/decrease

# 为什么使用tensorflow

- GPU加速 比cpu快很多

- 自动求导

- 神经网络API

> 给与cpu和gpu一个热身的时间：warm-up

数据分析的流程:

1. 提出问题
2. 准备数据
3. 分析数据
4. 获得结论
5. 成果可视化

### 对于LightGBM：又轻又快

在不降低准确率的前提下，速度提升了10倍左右，占用内存下降了3倍左右。因为它是基于决策树算法的，它采用最优的==叶明智==策略分裂叶子节点，然而它的提升算法分裂树一般采用的是深度方向或者水平明智。因此，当增长到相同的叶子节点，叶明智算法比水平-wise算法减少更多得损失。因此导致更高的精度。

J_\theta=-l(\theta)

### logistic函数：通过回归进行分类

### logistic回归的过程

- 1) 找到一个合适的预测函数，一般表示为h函数，该函数就是我们需要找的分类函数，它用来预测输入数据的判断结果。这个过程是非常关键的，需要对数据有一定的了解和分析，知道或者猜测预测函数的大概形式，比如是线性函数还是非线性函数。

- 2）构造一个loss损失函数，该函数表示预测的输出与训练数据类别之间的偏差。可以是二者之间的差或者是其他的形式。综合考虑所有训练数据的损失，将loss求和或者求平均，记为J(theta)函数，表示所有训练数据预测值与实际类别的偏差。

- 3）显然，J函数的值越小表示预测函数越准确。所以这一步需要做的是找到J函数的最小值。找到最小值有不同的方法。如梯度下降法。

# 线性回归

## 方程y=Ax

## 最小二乘法（平方）Least Squares Method

\sum_(n=1)^N（y-y_i）^2

w\hat=(\pmb{X^T}\pmb{X})^-1\pmb{X^T}y

> 让平方误差最小

集成算法

- bagging：套袋法

- boosting：提升算法：增大错误样本的权重同时减小正确样本的权重。与bagging对比boosting可以同时降低偏差和方差，而bagging只能降低模型的方差。但boosting更加容易过拟合。

- 随机森林：应用bagging和多颗决策树

- 梯度提升树

- adaboost：

> adaboost算法与boost算法不同，它是使用整个训练集来训练弱学习器，其中训练样本在每次迭代的过程中都会重新被赋予一个权重，在上一个弱学习器错误的基础熵进行学习来构建一个更加强大的分类器。

# sklearn学习

## 介绍

-  数据分析和数据挖掘

- 用python进行机器学习

> 数据分析和数据挖掘==机器学习==人工智能

## 分类

- classification

- regression

- clustring

- dimensionality reduction

- model selection

- preprocessing

控制流程：顺序、条件、循环

# 回归

## 一、线性回归

- 离散型数据：分类

- 连续型数据：回归

### y=kx+b

### 多个变量的情况