特征工程：

去中心化：让所有记录减去一个固定值。

数据归一化：把数据按照最小值中心化后再按极差缩放，然后被收敛到0-1之间

preprocessing.minmax

选择行，

选择列

选择行列

hist 直方图

from matplotlib import pyplot as plt

from matplotlib import font_manager

a=[zifuchuan]

plot.hist(a.fenzushu)

细节

计算组数=num_bin= (max(a)-nim(b)//d)

d=5

组数= 极差/组距

x轴的刻度设置

plt.xticks(range(min(a),max(a)+d,d))

plt.show()

图形大小：plt.figure(figsze=(20,8),dpi=80)

{数据}

数组的形状

shape即可查看数组的各个维度长度（输出按三维二维依次降低，块、行、个）

reshape方法可以重新设置行列，是有返回值的，而不改变本身

有返回值才会输出

结合shape和reshape可以做到在不清楚维度长度的情况下降维

flatten可以将数组展开变成一维

数组的计算

numpy数组对数字进行+*-/计算，是对全部单元进行计算

nan>>not a number 0/0

inf>>infinite x/0

数组对数组进行计算：

不同维度的数组进行计算至少有一个维度的长度相同

广播会在缺失或者长度为1的维度上进行（不同维度的计算本质上是广播）

广播原则：如果两个数组的后缘维度，即从末尾开始算起的维度轴长相符，或者某一方的长度为1，即广播jian'r

一维数组只有0轴，二维有0、1轴，三维有0、1、2轴

reshape(0,1,2)，shape输出(2,1,0)

CSV逗号分隔值文件

numpy的读取文件方法

unpack参数实现行列转置

transpose,T,swapaxes(1,0)方法实现行列转置

fsfada

numpy的索引和切片

索引从0开始

2:取得连续多行，[[2,5,6]]多一个[]取得不连续的行

:,1取得单列

:,1:取得连续列

:,[]取得不连续列

取得行列交叉的内容

取得不相邻的点

这个老师的逻辑能力和语言组织能力真的是匮乏 前言不搭后语 自己把自己绕进去了

讲的真垃圾

这课程讲的就和拿着稿子照本宣科一样

 #apply返回每个测试样本所在叶子节点的索引

clf.apply(xtext)

#predict返回每个测试样本的分类、回归结果

clf.predict(xtest)

#决策树
# from sklearn import tree#导入需要的模块
# clf=tree.DecisionTreeClassifier()#实例化
# clf=clf.fit(x_train,y_train)#用训练集数据训练模型
# result=clf.score(x_test,y_test)#导入测试集，从接口中调用需要的信息进行打分

citerion:不纯度，不纯的越低，训练集拟合越好

机器学习

支持向量机的分类方法，是在这组分布中找出一个超平面作为决策边界，使模型在数据上的 分类误差尽量接近于小，尤其是在未知数据集上的分类误差（泛化误差）尽量小。

决策边界一侧的所有点在分类为属于一个类，而另一侧的所有点分类属于另一个类。如果我们能够找出决策边界， 分类问题就可以变成探讨每个样本对于决策边界而言的相对位置。比如上面的数据分布，我们很容易就可以在方块 和圆的中间画出一条线，并让所有落在直线左边的样本被分类为方块，在直线右边的样本被分类为圆。如果把数据 当作我们的训练集，只要直线的一边只有一种类型的数据，就没有分类错误，我们的训练误差就会为0。

但是，对于一个数据集来说，让训练误差为0的决策边界可以有无数条。

支持向量机（SVM，也称为支持向量网络），是机器学习中获得关注最多的算法没有之一。它源于统计学习理论， 是我们除了集成算法之外，接触的第一个强学习器。它有多强呢？

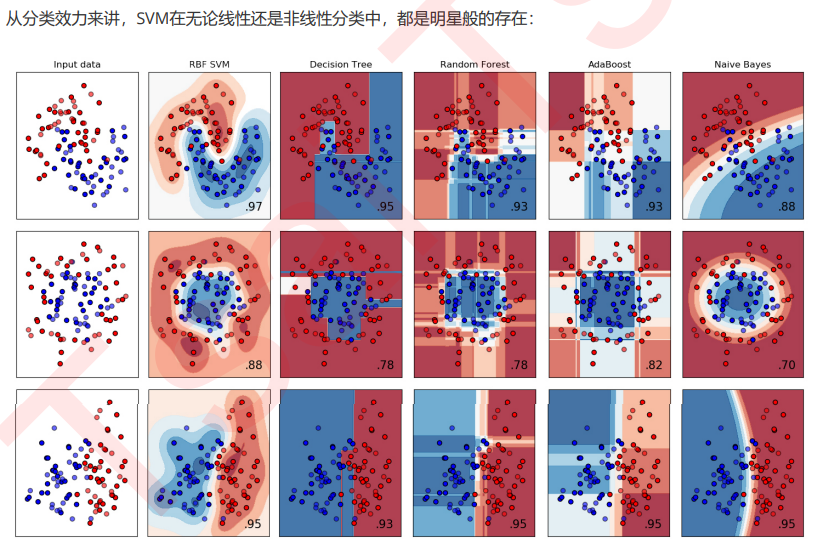
从实际应用来看，SVM在各种实际问题中都表现非常优秀。它在手写识别数字和人脸识别中应用广泛，在文本和超 文本的分类中举足轻重，因为SVM可以大量减少标准归纳（standard inductive）和转换设置（transductive settings）中对标记训练实例的需求。同时，SVM也被用来执行图像的分类，并用于图像分割系统。。除此之外，生物学和许多其他科学都是SVM的青睐者，SVM现在已经广泛被用于蛋白质分类，现 在化合物分类的业界平均水平可以达到90%以上的准确率。在生物科学的尖端研究中，人们还使用支持向量机来识 别用于模型预测的各种特征，以找出各种基因表现结果的影响因素。

从学术的角度来看，SVM是最接近深度学习的机器学习算法。线性SVM可以看成是神经网络的单个神经元（虽然损 失函数与神经网络不同），非线性的SVM则与两层的神经网络相当，非线性的SVM中如果添加多个核函数，则可以 模仿多层的神经网络。

高效嵌入法embedded

业务选择

说到降维和特征选择，首先要想到的是利用自己的业务能力进行选择，肉眼可见明显和标签有关的特征就是需要留 下的。当然，如果我们并不了解业务，或者有成千上万的特征，那我们也可以使用算法来帮助我们。或者，可以让 算法先帮助我们筛选过一遍特征，然后在少量的特征中，我们再根据业务常识来选择更少量的特征。

PCA和SVD一般不用

逻辑回归是由线性回归演变而来，线性回归的一个核心目的是通过求解参数来探究特征X与标签y之间的 关系，而逻辑回归也传承了这个性质，我们常常希望通过逻辑回归的结果，来判断什么样的特征与分类结果相关， 因此我们希望保留特征的原貌。PCA和SVD的降维结果是不可解释的，因此一旦降维后，我们就无法解释特征和标 签之间的关系了。当然，在不需要探究特征与标签之间关系的线性数据上，降维算法PCA和SVD也是可以使用的。

统计方法可以使用，但不是非常必要

逻辑回归对数据的要求低于线性回归，由于我们不是使用最小二乘法来求解，所以逻辑回归对数据的总体分布和方差没有要求，也不需要排除特征之间的共线性，但如果我 们确实希望使用一些统计方法，比如方差，卡方，互信息等方法来做特征选择，也并没有问题。过滤法中所有的方法，都可以用在逻辑回归上。

重要参数penatly&C

1、正则化

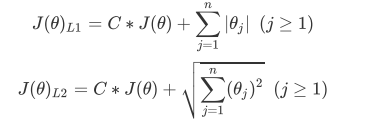
L1正则化和L2正则化虽然都可以控制过拟合，但它们的效果并不相同。当正则化强度逐渐增大（即C逐渐变小）， 参数的取值会逐渐变小，但L1正则化会将参数压缩为0，L2正则化只会让参数尽量小，不会取到0。

在L1正则化在逐渐加强的过程中，携带信息量小的、对模型贡献不大的特征的参数，会比携带大量信息的、对模型 有巨大贡献的特征的参数更快地变成0，所以L1正则化本质是一个特征选择的过程，掌管了参数的“稀疏性”。L1正 则化越强，参数向量中就越多的参数为0，参数就越稀疏，选出来的特征就越少，以此来防止过拟合。

相对的，L2正则化在加强的过程中，会尽量让每个特征对模型都有一些小的贡献，但携带信息少，对模型贡献不大 的特征的参数会非常接近于0。通常来说，如果我们的主要目的只是为了防止过拟合，选择L2正则化就足够了。但 是如果选择L2正则化后还是过拟合，模型在未知数据集上的效果表现很差，就可以考虑L1正则化。