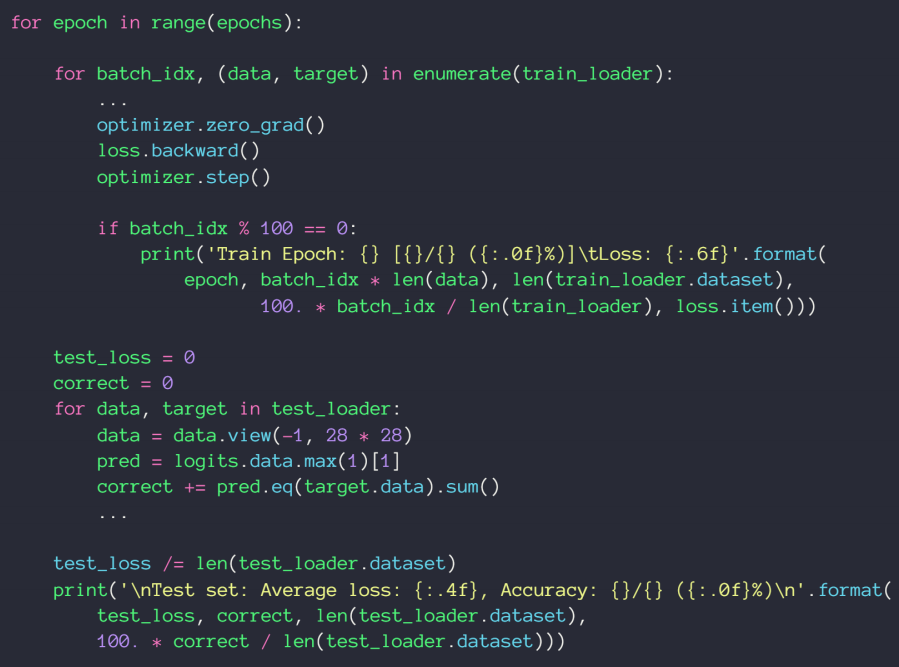
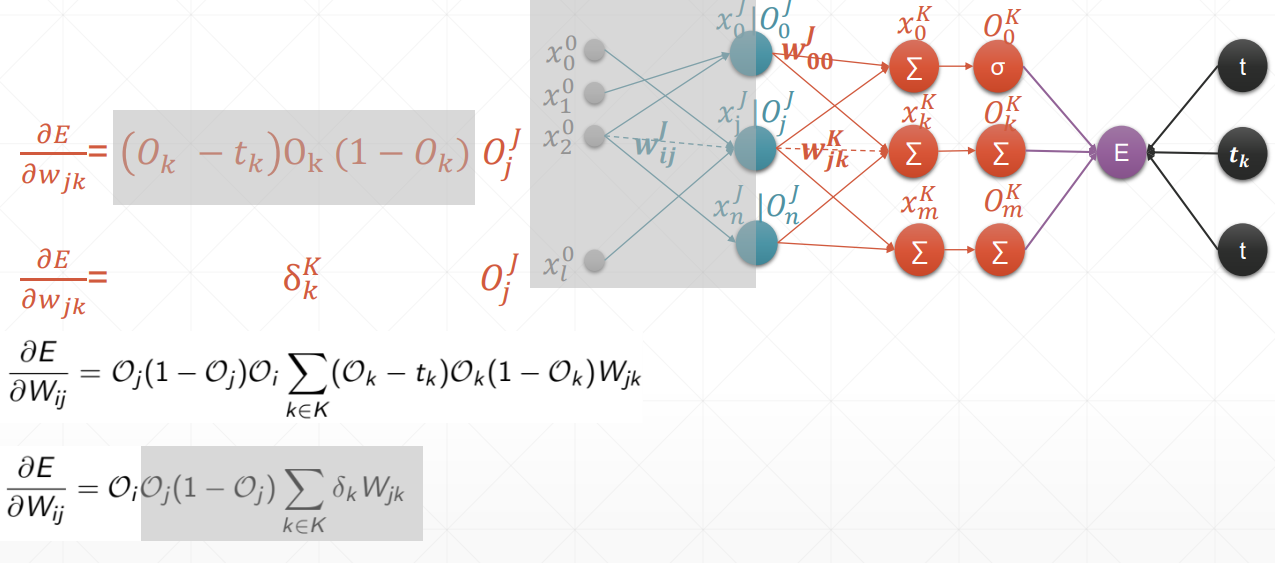
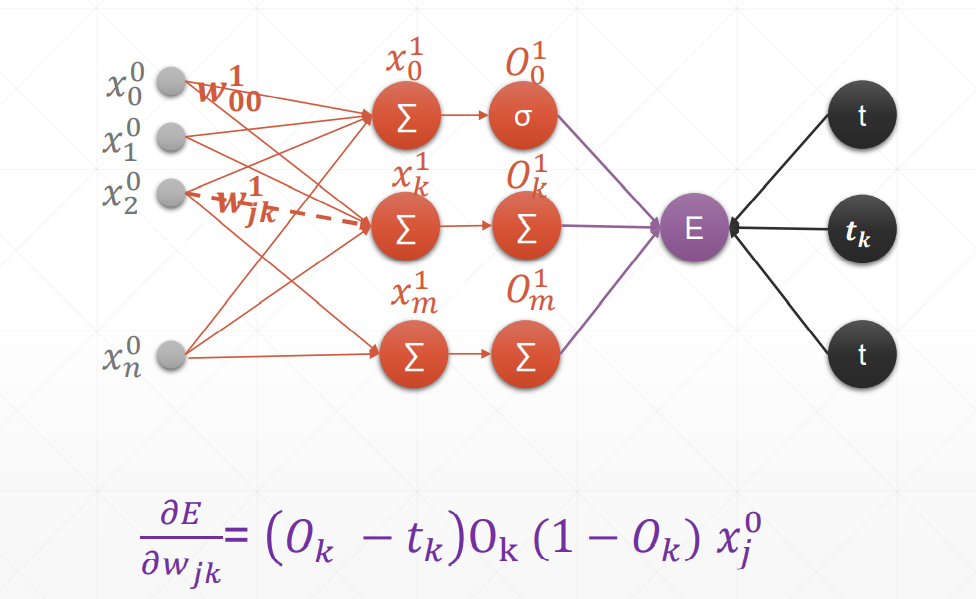
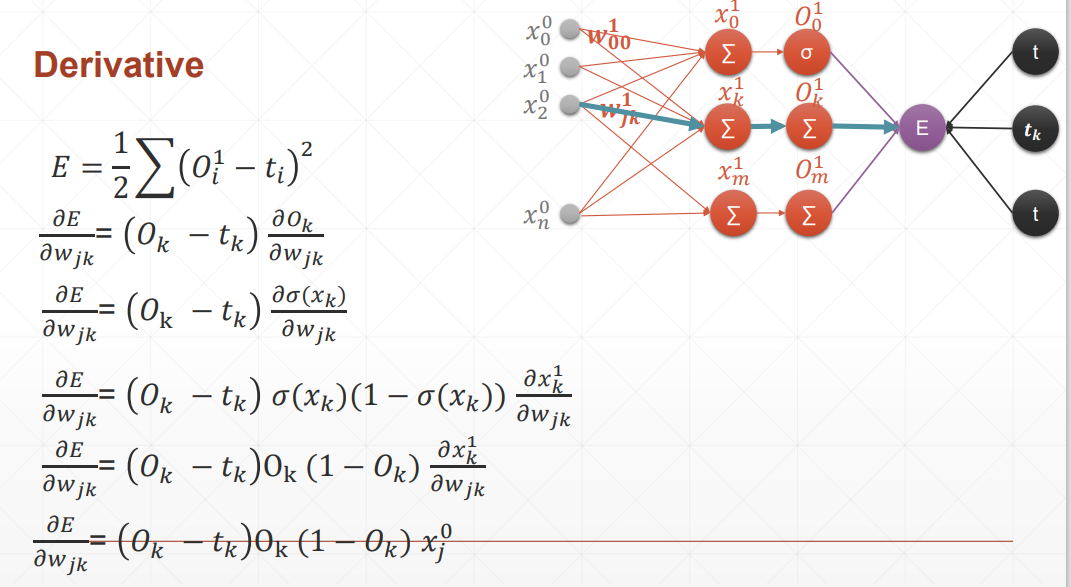
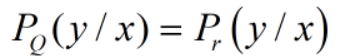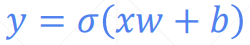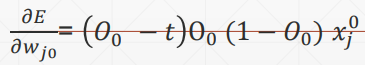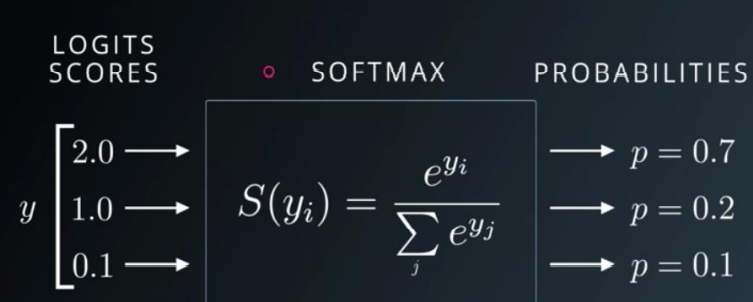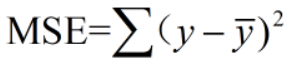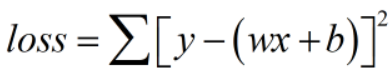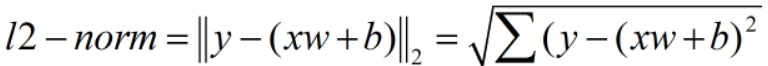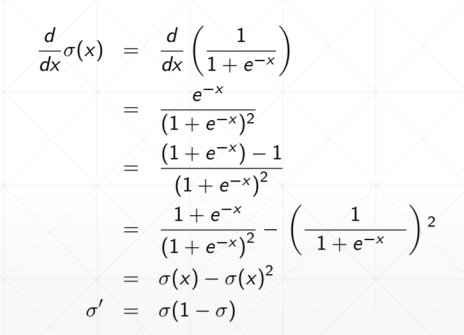动量和学习率衰减
动量——惯性
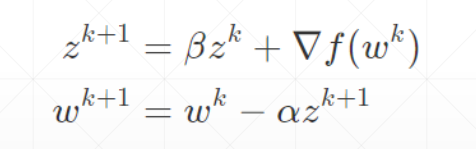
动量是考虑了之前的运动方向的变量
不考虑动量的情况下,会在局部极小值点停止
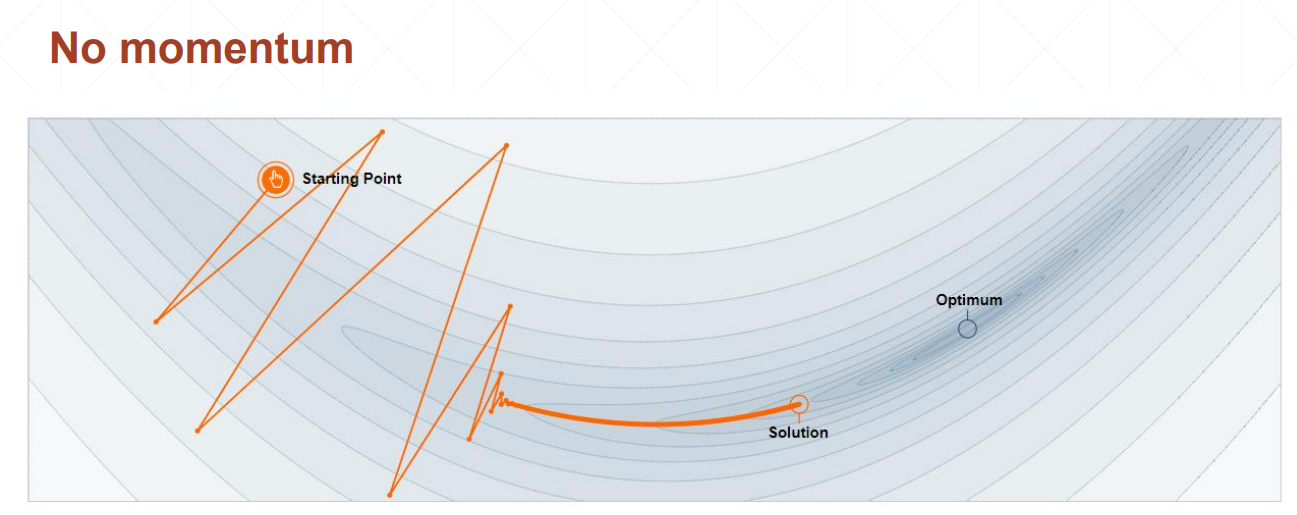
考虑动量的情况下,在局部极小值点处仍然会向前走,比较容易找到全局最优解

优化器中SGD没有考虑动量,可以自己加momentum参数,Adam里面考虑了动量因素,不需要手动加

学习率衰减——迫使学习率逐渐变为0

这这里我们并不能指明最合适的学习率,但我们可以让学习率递减,好处是可以较快得找到更好的解
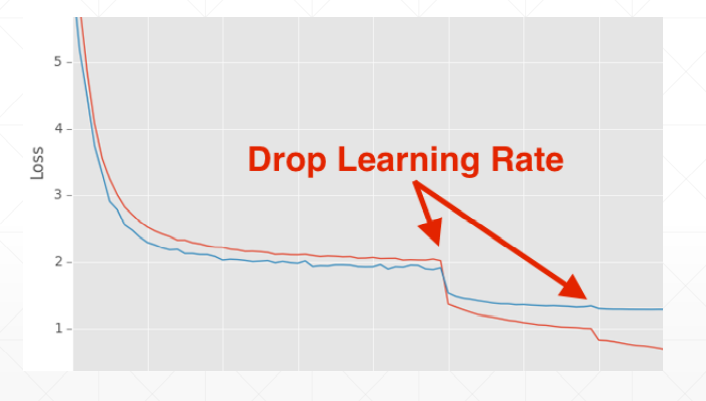
方法一:使用ReducelROnPlateau()函数,传入optimizer 和min,前者用来识别学习率的值,后者用来监听loss,当在某一个学习率上在一定的步长范围内,loss都没有很明显的变化,我们的函数将会自动调整学习率;

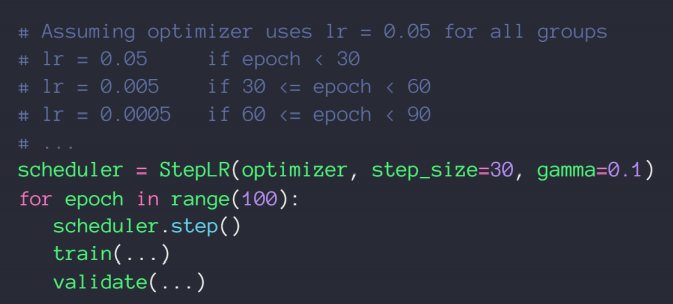
方法二:直接规定一个确切步长,确定一个变化率