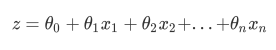
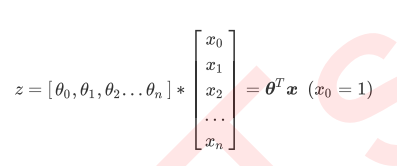
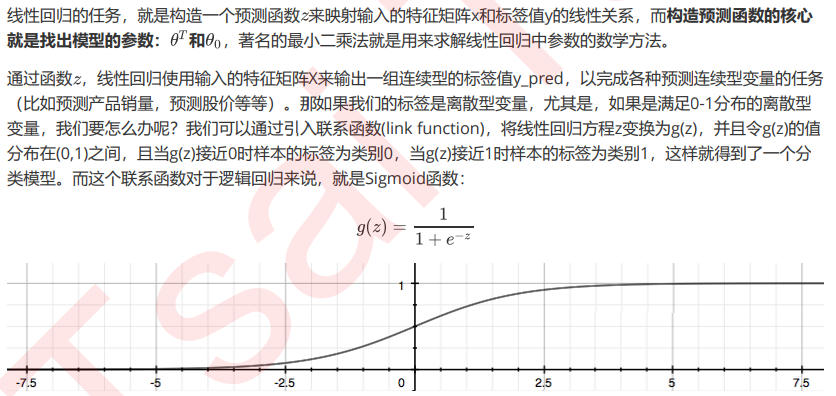
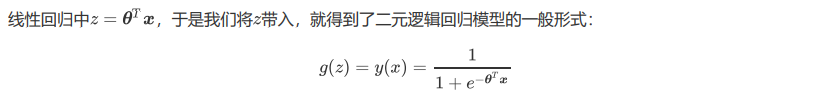
而逻辑回归，是一种名为“回归”的线性分类器，其本质是由线性回 归变化而来的，一种广泛使用于分类问题中的广义回归算法。要理解逻辑回归从何而来，得要先理解线性回归。线 性回归是机器学习中最简单的的回归算法，它写作一个几乎人人熟悉的方程：

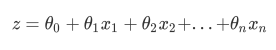
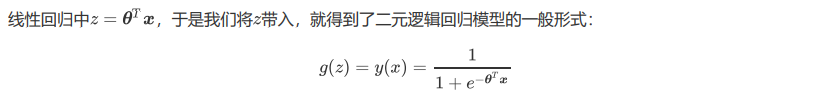
传递不可变对象

不可变对象：int、float、字符串、元组、布尔值

在赋值操作时会创建一个对象。

参数的传递：从实参到形参的赋值操作。

所有的赋值操作都是”引用的赋值“,Python中参数的传递都是“引用传递”，不是“值传递”。

可变对象：字典、列表、集合、自定义的对象

局部变量和全局变量效率测试

局部变量的查询和访问速度比全局变量快，优先考虑局部变量。

变量的作用域（全局变量和局部变量）

全局变量：作用域为定义的模块。（少定义）（作为常量）（函数内部想改变全局变量的值，使用global声明一下）

局部变量：作用域为函数体。在栈的栈帧中，调用完函数就删除。

函数也是对象，内存底层分析

对象：堆里面的内存块

def:在堆里创建函数对象

同时在栈里创建对象名字是函数名称，值为函数地址，进行调用时，函数名称（），表示调用函数，顺着地址找到函数进行调用，创建一次调用多次，

形参和实参

文档字符串（函数的注释）

函数用法和底层分析

函数是可重用的程序代码块。python中，定义函数的语法如下：

def 函数名（[参数列表]）：

      '''文档字符串'''

      函数体/若干语句

要点：

       使用def来定义函数，def之后是空格，然后是函数名和()，Python执行def时，会创建一个函数对象，并绑定到函数名变量上。

推导式创建序列

列表推导式

列表推导式生成列表对象，语法如下：

    [表达式  for   item   in    可迭代对象]

字典推导式

    {key:value  for  value  for  表达式  in  可迭代对象}

集合推导式

    {表达式 for  item   in  可迭代对象}

生成器推导式（用于生成元组）

一个生成器只能运行一次，用过不可再用。

使用zip()并行迭代

zip()函数对多个序列进行迭代

循环代码优化（循环次数较多）

（1）尽量减少循环内部不必要的运算。

（2）嵌套循环中，尽量减少内层循环的计算，尽可能向外提。

（3）局部变量查询较快，尽量使用局部变量。

（4）连接多个字符串，使用join而不使用+

（5）列表进行元素插入和删除，尽量在尾部jin'xing

else语句

while、for循环可以附带一个else语句（可选）。如果for、while语句没有被break语句结束，则会执行else子句。否则不执行。

重要属性components_

通常来说，在新的特征矩阵生成之前，我们无法知晓PCA都建立了怎样的新特征向量，新 特征矩阵生成之后也不具有可读性，我们无法判断新特征矩阵的特征是从原数据中的什么特征组合而来，新特征虽 然带有原始数据的信息，却已经不是原数据上代表着的含义了。

但是其实，在矩阵分解时，PCA是有目标的：在原有特征的基础上，找出能够让信息尽量聚集的新特征向量。

如果原特征矩阵是图像，V(k,n)这 个空间矩阵也可以被可视化的话，我们就可以通过两张图来比较，就可以看出新特征空间究竟从原始数据里提取了 什么重要的信息。

PVC中的SVD

重要参数svd_solver 与 random_state

"auto"：基于X.shape和n_components的默认策略来选择分解器：如果输入数据的尺寸大于500x500且要提 取的特征数小于数据最小维度min(X.shape)的80％，就启用效率更高的”randomized“方法。否则，精确完整 的SVD将被计算，截断将会在矩阵被分解完成后有选择地发生。

"full"：从scipy.linalg.svd中调用标准的LAPACK分解器来生成精确完整的SVD，适合数据量比较适中，计算时 间充足的情况，生成的精确完整的SVD的结构为：

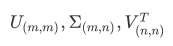
"arpack"：从scipy.sparse.linalg.svds调用ARPACK分解器来运行截断奇异值分解(SVD truncated)，分解时就将特征数量降到n_components中输入的数值k，可以加快运算速度，适合特征矩阵很大的时候，但一般用于 特征矩阵为稀疏矩阵的情况，此过程包含一定的随机性。截断后的SVD分解出的结构为：

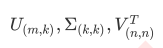
"randomized"，通过Halko等人的随机方法进行随机SVD。在"full"方法中，分解器会根据原始数据和输入的 n_components值去计算和寻找符合需求的新特征向量，但是在"randomized"方法中，分解器会先生成多个随机向量，然后一一去检测这些随机向量中是否有任何一个符合我们的分解需求，如果符合，就保留这个随 机向量，并基于这个随机向量来构建后续的向量空间。这个方法已经被Halko等人证明，比"full"模式下计算快 很多，并且还能够保证模型运行效果。适合特征矩阵巨大，计算量庞大的情况。

重要参数n_components

n_components是我们降维后需要的维度，即降维后需要保留的特征数量，降维流程中第二步里需要确认的k值， 一般输入[0, min(X.shape)]范围中的整数。K是一个需要我们人为去确认的超参数，并且我们设定的数字会影响到模型的表现。就达不到降维的效果，如果留下的特征太少，那新特征向量可能无法容纳原始数据集中的大部分信息，因此，n_components既不能太大也不能太小。那怎么办呢？

可以先从我们的降维目标说起：如果我们希望可视化一组数据来观察数据分布，我们往往将数据降到三维以下，很 多时候是二维，即n_components的取值为2。

PCA使用的信息量衡量指标，就是样本方差，又称可解释性方 差，方差越大，特征所带的信息量越多。

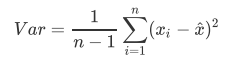
下去补补数学知识吧···

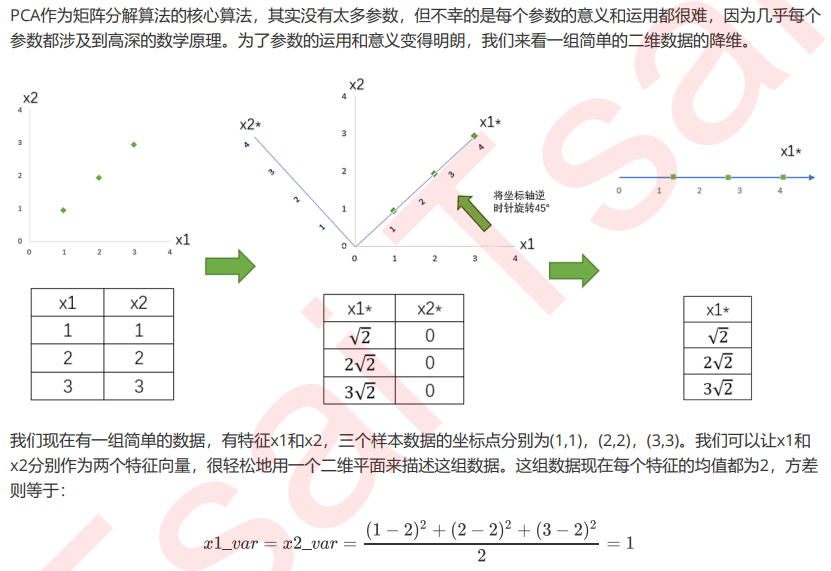
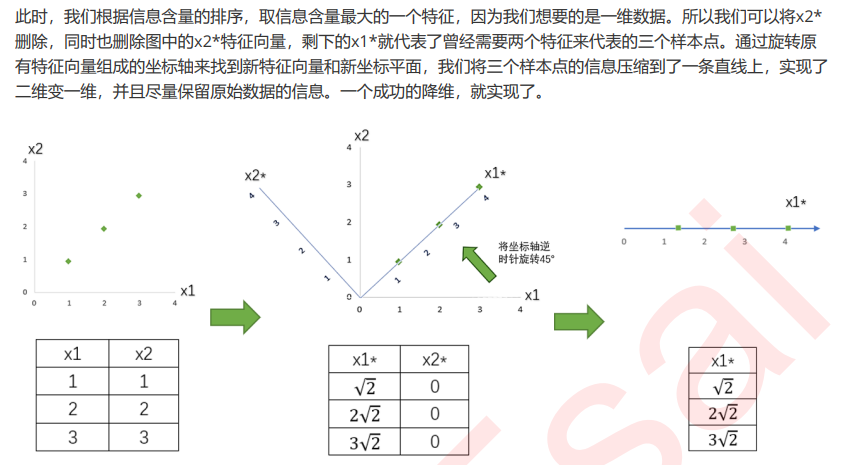
将为过程的主要步骤如下：

思考：PCA和特征选择技术都是特征工程的一部分，它们有什么不同？

特征工程中有三种方式：特征提取，特征创造和特征选择。仔细观察上面的降维例子和上周我们讲解过的特征 选择，你发现有什么不同了吗?

特征选择是从已存在的特征中选取携带信息最多的，选完之后的特征依然具有可解释性，我们依然知道这个特 征在原数据的哪个位置，代表着原数据上的什么含义。

而PCA，是将已存在的特征进行压缩，降维完毕后的特征不是原本的特征矩阵中的任何一个特征，而是通过某 些方式组合起来的新特征。通常来说，在新的特征矩阵生成之前，我们无法知晓PCA都建立了怎样的新特征向 量，新特征矩阵生成之后也不具有可读性，我们无法判断新特征矩阵的特征是从原数据中的什么特征组合而 来，新特征虽然带有原始数据的信息，却已经不是原数据上代表着的含义了。以PCA为代表的降维算法因此是 特征创造（feature creation，或feature construction）的一种。

可以想见，PCA一般不适用于探索特征和标签之间的关系的模型（如线性回归），因为无法解释的新特征和标 签之间的关系不具有意义。在线性回归模型中，我们使用特征选择。

break语句

break语句可用于while和for循环，用来结束整个循环，当有嵌套循环时，break语句只能跳出最近一层的循环。

continue语句

continue语句用于结束本次循环，继续下一次，多个循环嵌套时，continue也是应用于最近的一层循环。

嵌套循环

for循环和可迭代对象遍历

for循环通常用于可迭代对象的遍历，语法格式如下：

for 变量 in 可迭代对象：

       循环体语句

循环结构

while循环