很不错的例子，肺癌

提升：

梯度提升

SST (总方差)= SSE() + SSR （残差平方和）

只有无偏估计下成立，否则 SST≥SSE+ SSR

局部加权

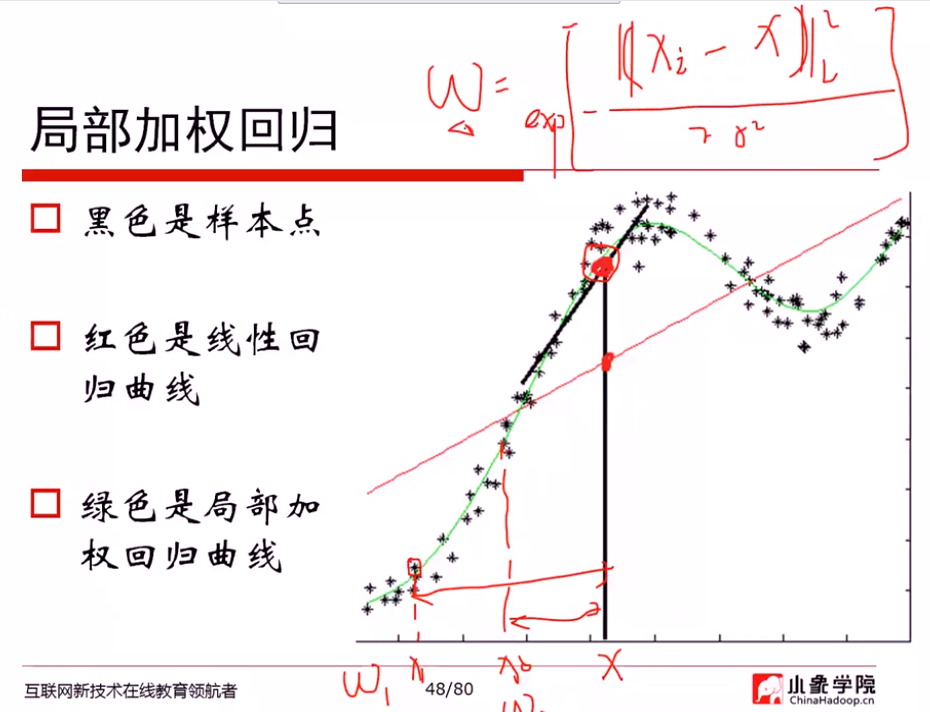
最重要的问题: 如何度量权重

Logistic回归

p(y|x:θ)  y=0, y=1时,写成上述密度函数形式

解法1: 从mle求解

极大似然估计的梯度上升算法，本质与梯度下降无区别，梯度上升取正梯度方向，同样设置步长a；梯度下降选取负梯度方向，

线性回归:  假定服从高斯分布，通过MLE进行估计

logistics回归: 假定服从二项分布，通过MLE进行估计

如果都进行梯度下降法估计，会发现求解的方式都是一样的

广义线性模型的定义: 因变量不服从正态分布，且因变量与自变量不存在线性关系；广义就是要找一个非线性的关系f，使得转换后更接近因变量的分布

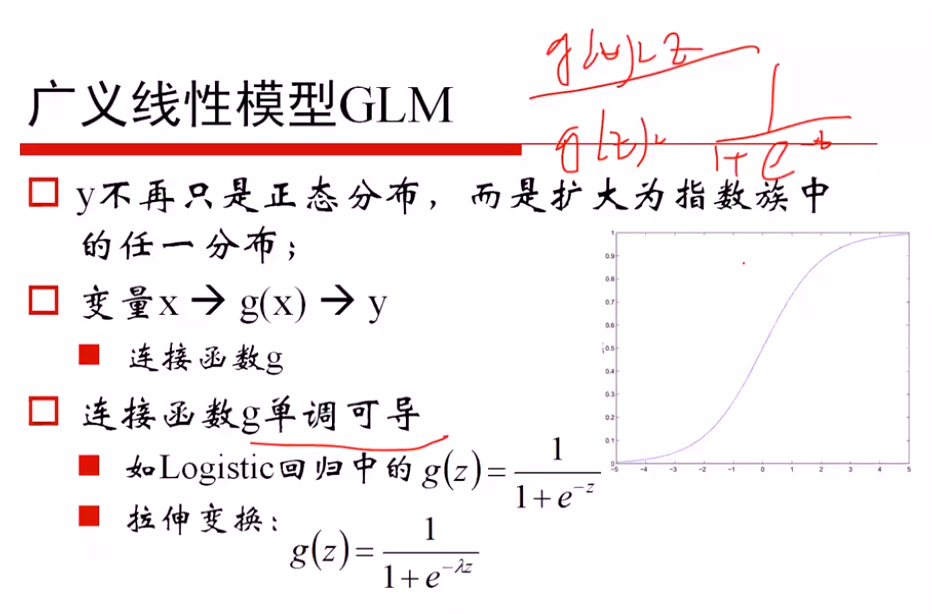
证明是一个广义的线性模型:

对数线性模型:

从对数模型理解 logistics函数

一方面: 从 ln(p/(1-p)) = θx 推导出 p = logistics函数，说明希望对数模型是线性的，从而推导出概率可以用logistics函数表示

另一方面: 从 p=logistics函数 + ln(p/(1-p))对数模型，推导出对数模型是线性的θTx

广义线性模型  → 相似的梯度下降方法

解法2: 从损失函数进行求解

(1)对 -1, 1转换为0, 1  进行(yi+1)/2...

softmax回归

鸢尾花数据

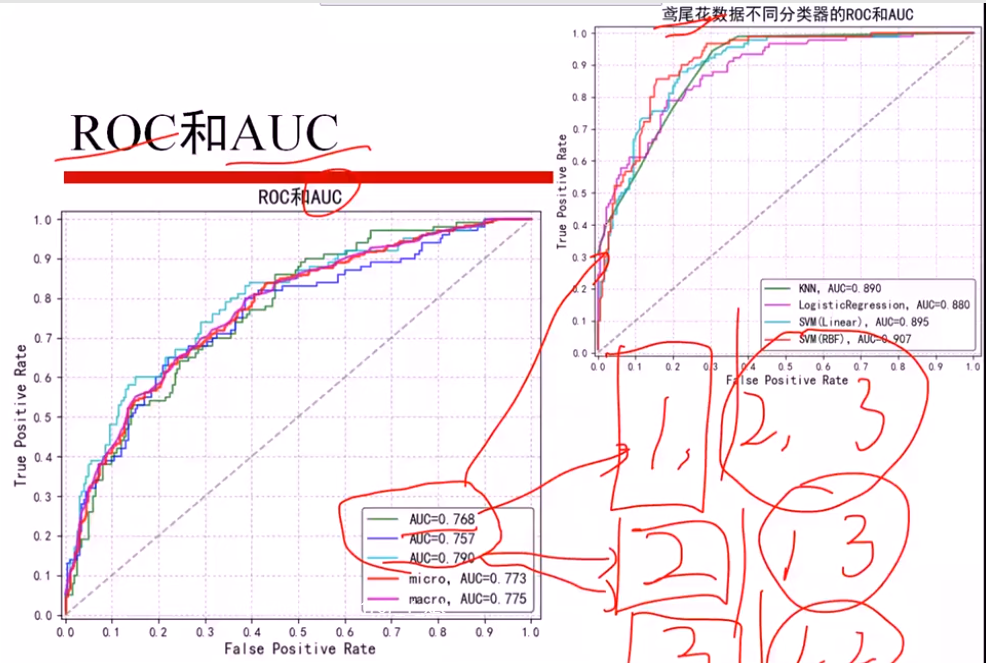
分为三个 二分类问题，算出三个AUCi值

micro: 直接算三个平均AUCi，得出AUC

macro: 总体加和，当作一个AUC计算

1. 线性回归

• 极大似然估计解释最小二乘

假设: 误差ξ服从高斯分布(0, δ)

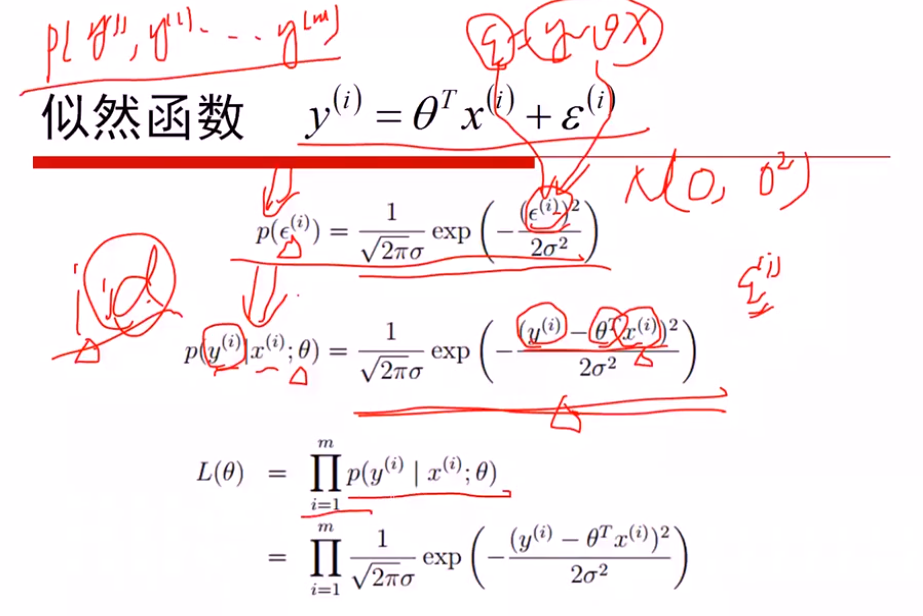
①最大化似然函数，对l(θ)进行简化

max l(θ)  等价于 min(J(θ))

• 1 最小二乘的矩阵推导

注意:

(1)是关于θ的函数，最大化θ参数

(2)J(θ)是一个xTx的凸函数，因为xTx是半正定的，开口向上，xTxθTθ就是关于θ的开口向上的二次函数

• 线性回归复杂度惩罚因子

（1）L2正则，进行对θ惩罚 -- Ridge回归

         L1正则，  --  Lasso回归

• 解释为什么L1有特征选择能力:

1 拉格朗日角度进行解释

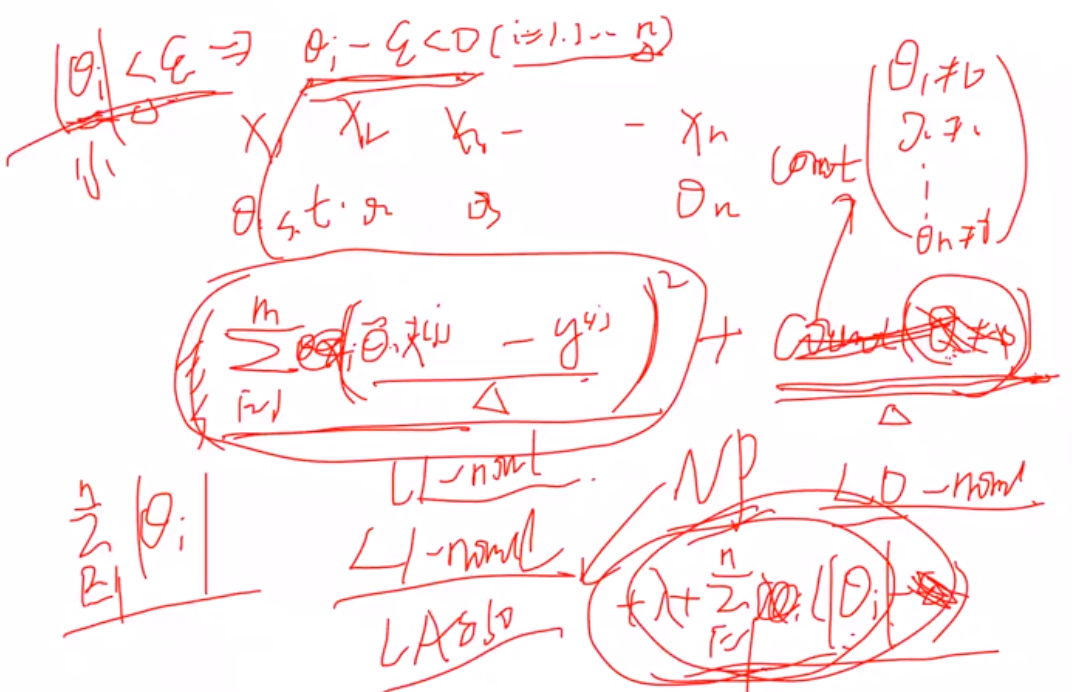
（1） 原本的目标: 希望θ=0就计0，不等于0就计为1，惩罚θ>0时候的数目，但是由于是无解的，因此用L1范数进行近似

推导看手稿:

2 几何解释:

L1约束使得某一个wi是0，稀疏约束

L2使得两个wi都比较小，约束

• L1正则不可导如何解决?

(1)坐标轴下降法

(2)近端梯度近似法...  其余还有很多

• 2 广义逆矩阵求解（伪逆）

（1）当x可逆， θx =y可以直接进行求解，不用进行目标函数最小化求解，因此可以利用SVD进行奇异值分解，求出伪逆矩阵后进行求解 

• 3 梯度下降法求解

1. Logistics 回归
2. 多分类softmax回归
3. 技术:

• 梯度下降
• 最大似然估计
• 特征选择

1. 1 贝叶斯, MLE的思想

假设1：p(Ai) 概率相似

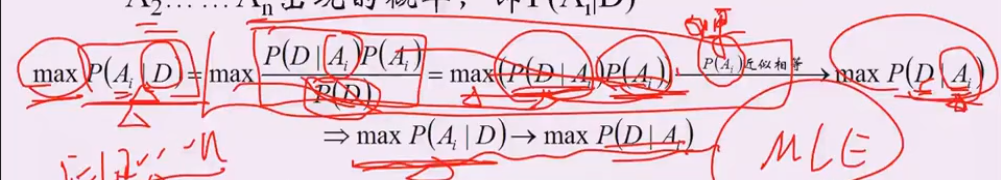
P（D|Ai)： 给定结论Ai下， 这个数据以多大的概率产生。 可以理解为x1..xn是未知的数据参数，θi是已知的参数，能够使  p(x1..xn|θi)最大的参数θi，就是我们想要估计的参数， 这里xi对应D，Ai对应参数θ

1. 2 赔率分析

公平赔率； y = 1/p   y是赔率，p是赢的概率

赔率公式    y =a/p

计算庄家盈亏:

10.5% = 0.21 a / 2a

1. 3 模糊查询与替换

2 PCA

2.1 原理

①求协方差矩阵

② 特征值排序

③ 方差最大的就认为是主要的方向，其中特征向量相互垂直，每一个特征向量就是一个方向，Aμi的方差最大，就认为是最主要的投影方向

①假定样本已经作了中心化，所以忽略均值E

Q 为什么特征值最大 等价于 求方差最大？

PCA中希望投影的方差最大，认为得到的信息最多。

目标函数: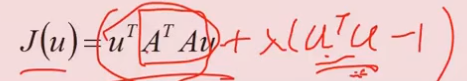

加上等式约束  μTμ=1， 根据拉格朗日求解，

aJ/aμ = 2ATAμ +2λμ = 0 ,求得λ就是 ATA的特征值。

因此，方差最大 等价于 最大特征值

2.2 过拟合问题

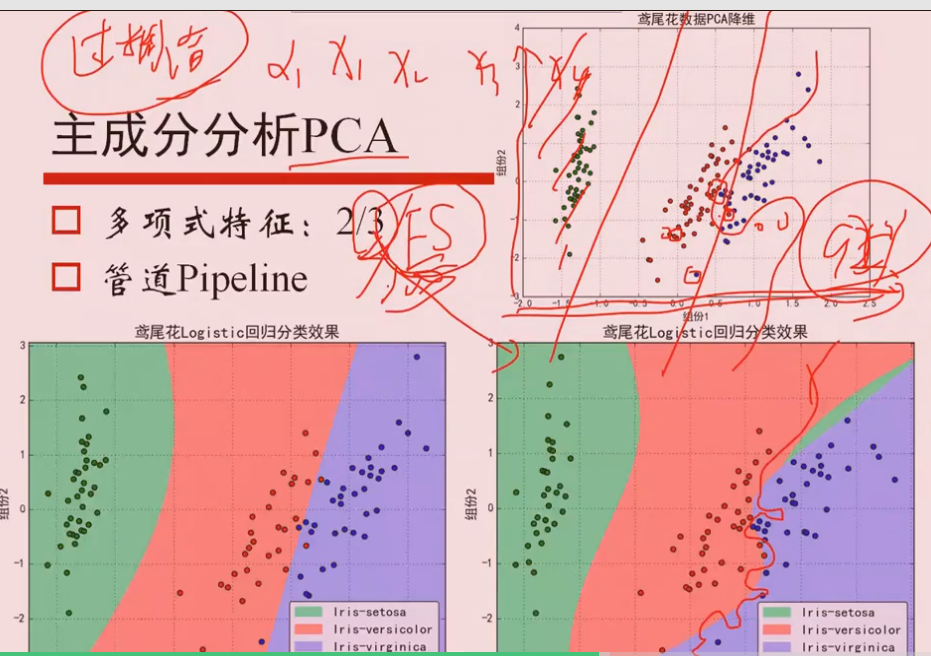
使用高阶的特征x1^2, x2^2...，特征过多，虽然会得到弯曲的曲线进行分离，但是很有可能产生过拟合问题

决策树不需要做one-hot编码

6.1 Prime

计算素数:  

fliter(函数, x): 把数字放入x中，结果输出

1、sgd:随机梯度下降（）

2、bgd：

3、min-batch:

4、在线学习的好处。样本

# 回归

## 一、线性回归

- 离散型数据：分类

- 连续型数据：回归

### y=kx+b

### 多个变量的情况

# 数据清洗和特征选择

## fuzzeywuzzy模糊查询

- 任何一次插入，修改和删除算作一次过程+1