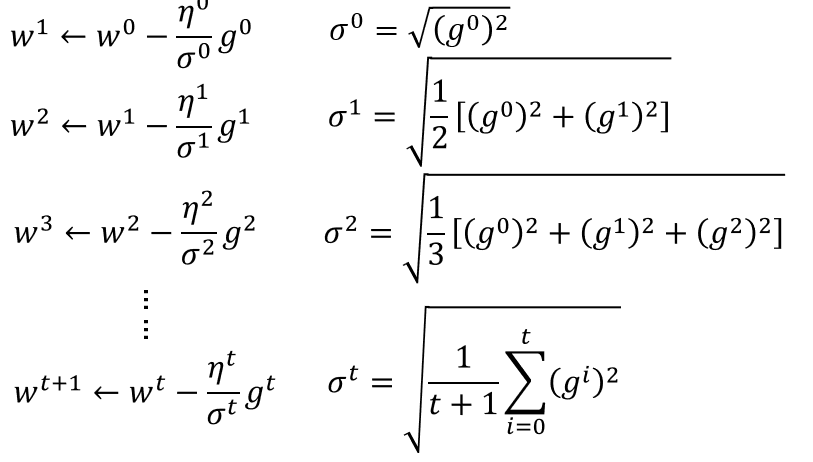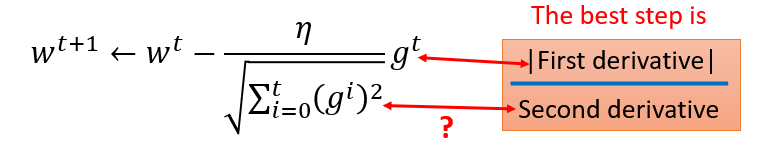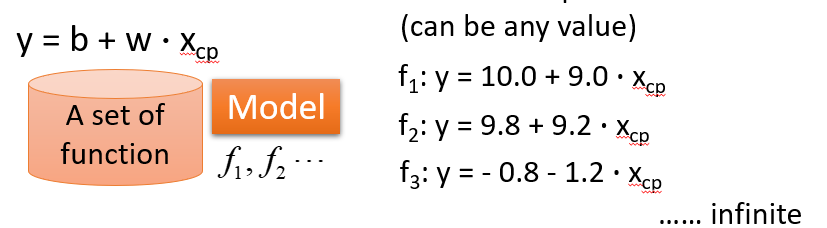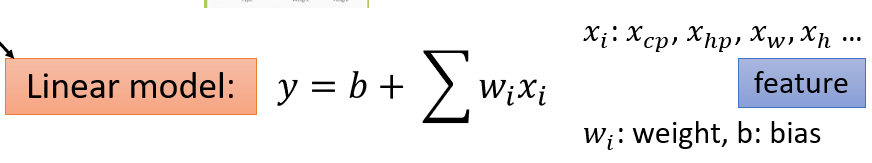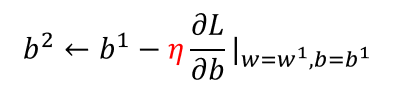x_i: features
input: x^n
output: y^^n
function: f_n
Loss function L(function 的 function):
- Input: a function
- Output: how bad it is
- L(f) = L(w, b)
Step3: Best Function
f* = arg min L(f)
w*, b* = arg min L(w, b)
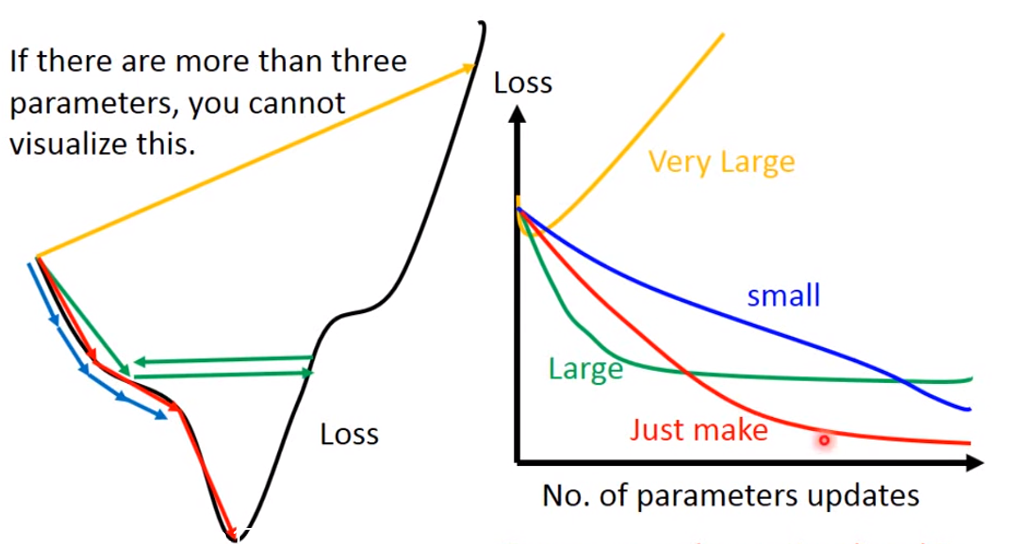
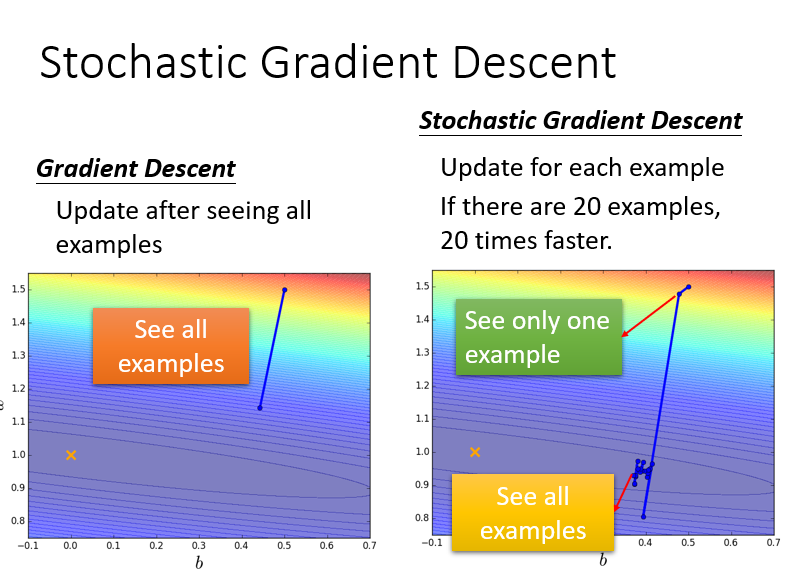
Gradient Descent:
- initial value w^0
- dL/dw|w=w^0
- 若 negative,增加 w
- 若 positive,减小 w
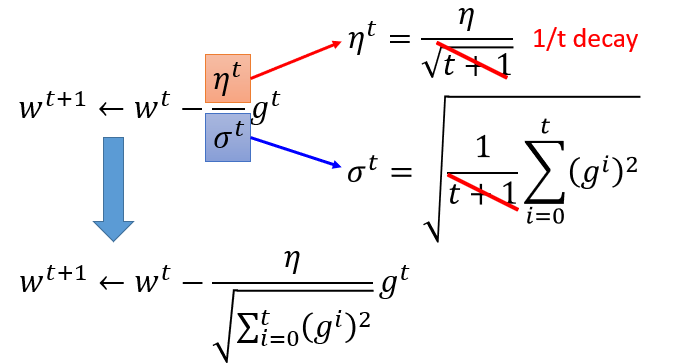
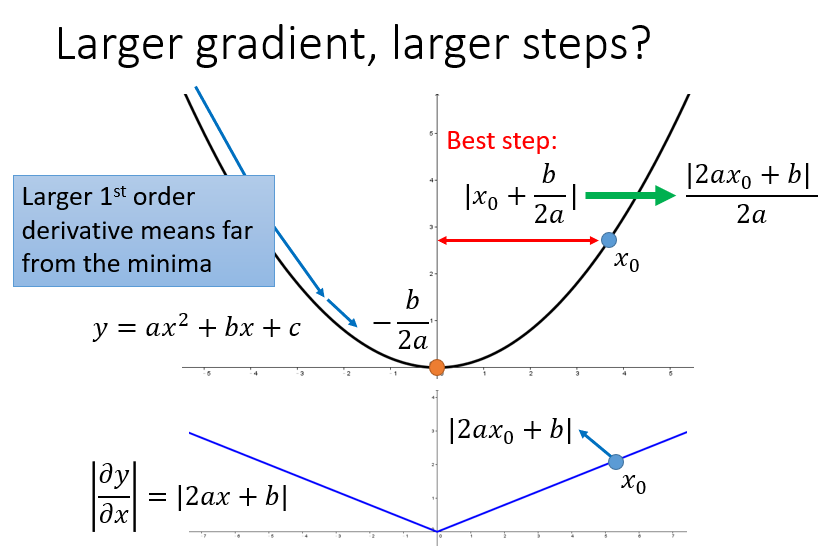
- η(learning rate): 参数更新的幅度 -η(dL/dw|w=w^0)
- Local optimal: 局部最优
- global optimal: 全局最优
- 两个参数 w, b: 分别对 w, b 求偏微分
- ▽L: gradient 梯度
convex 凸面的 adj.
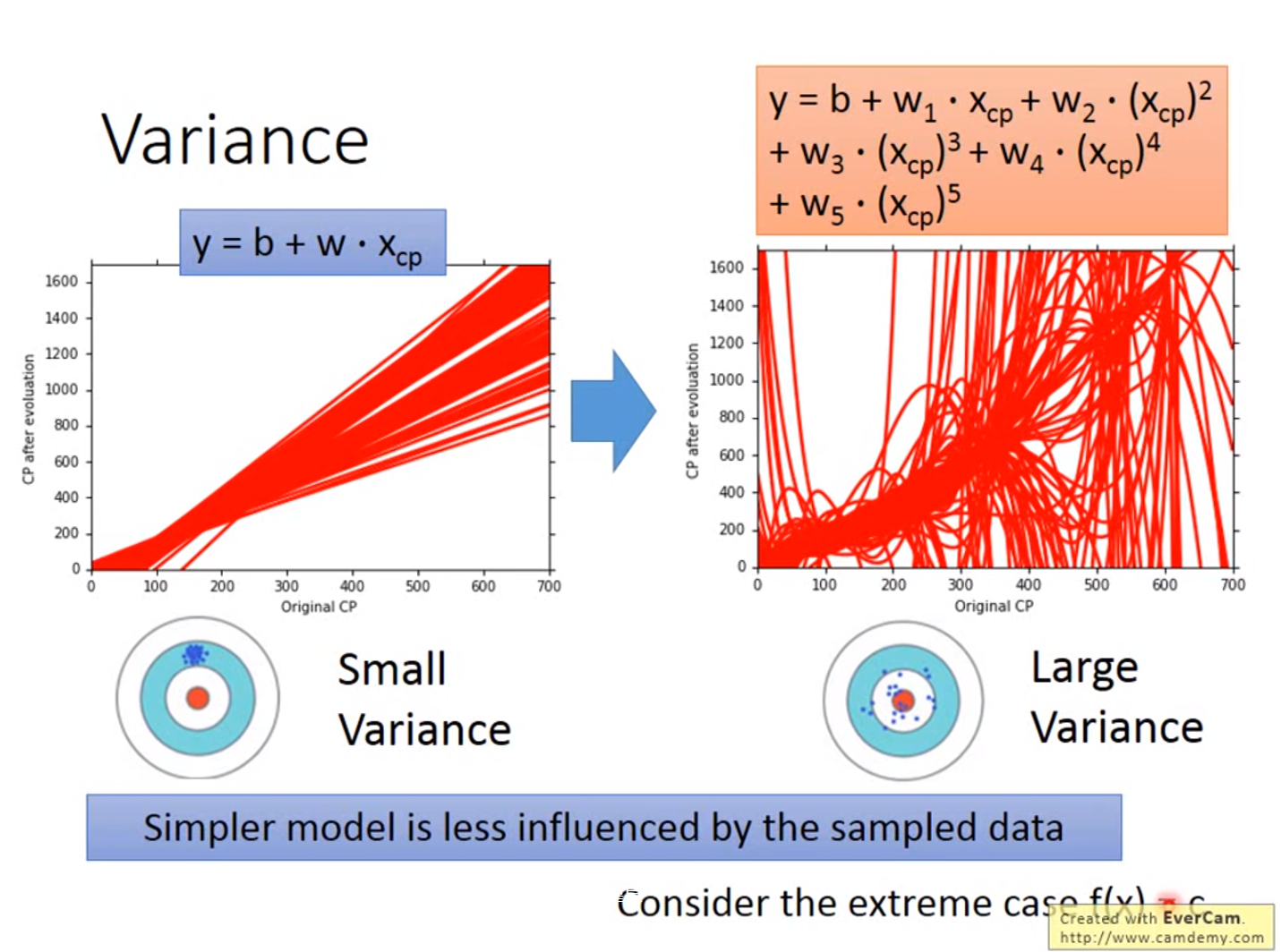
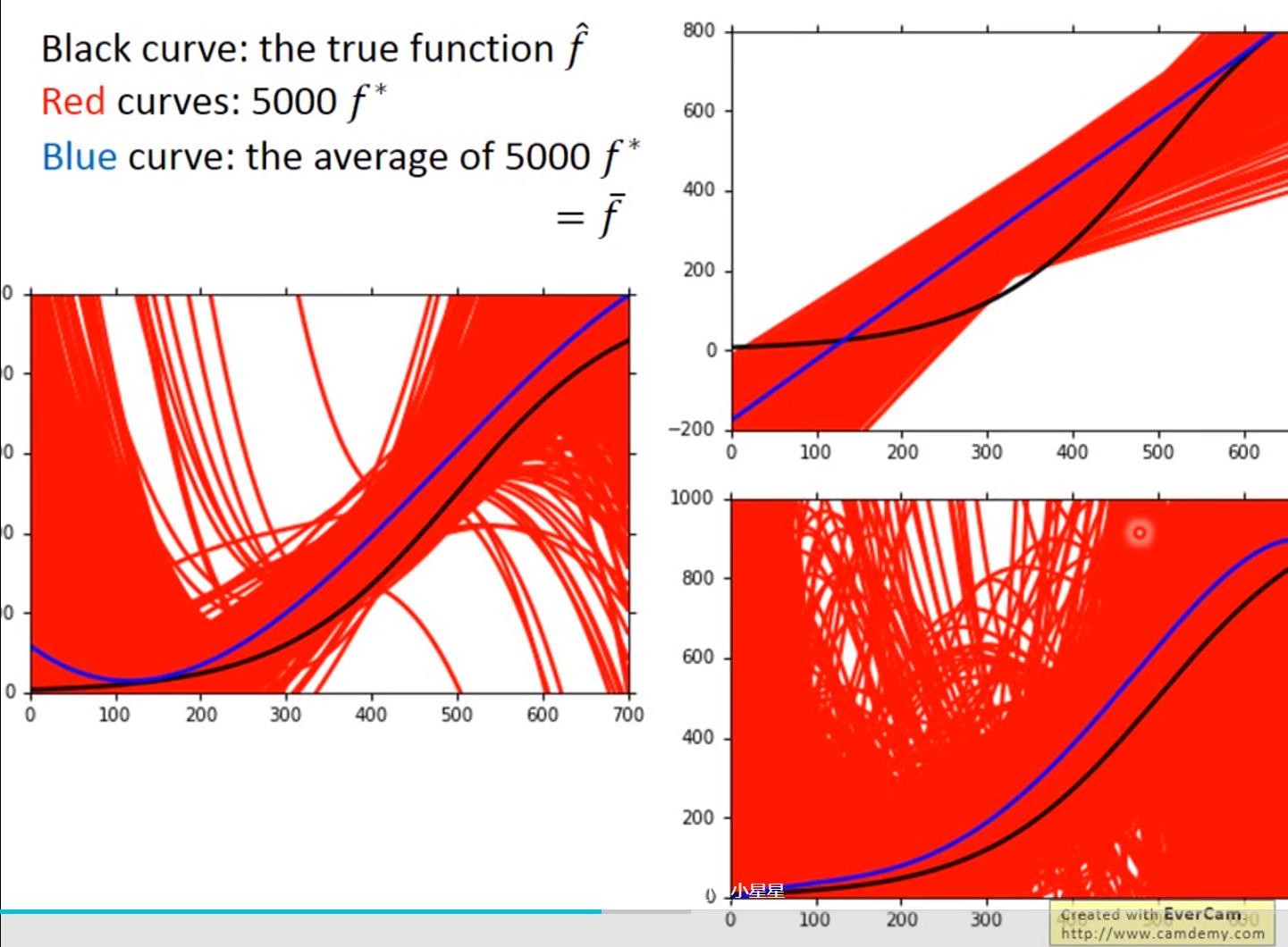
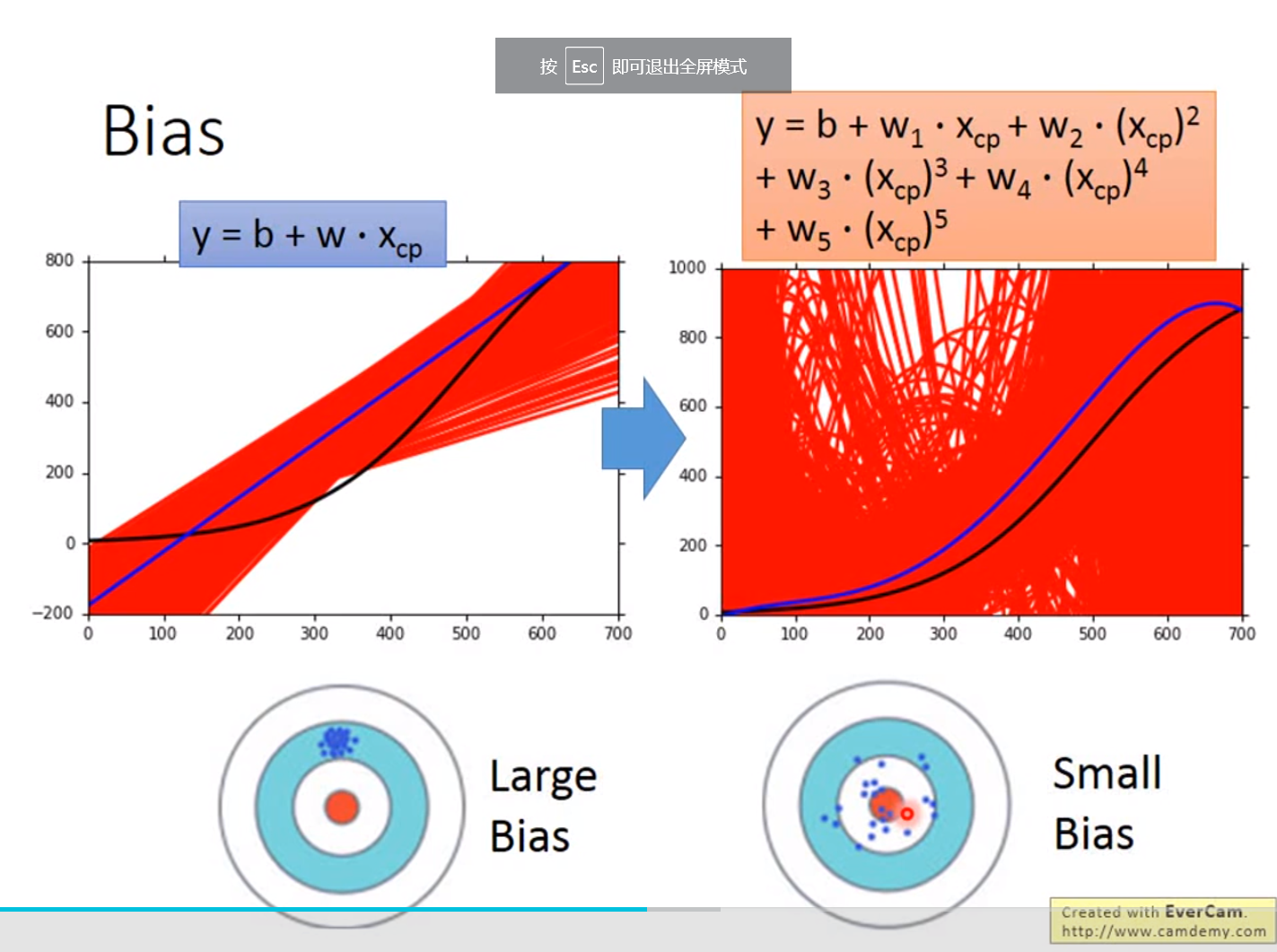
引入更复杂的函数:
x_cp^2
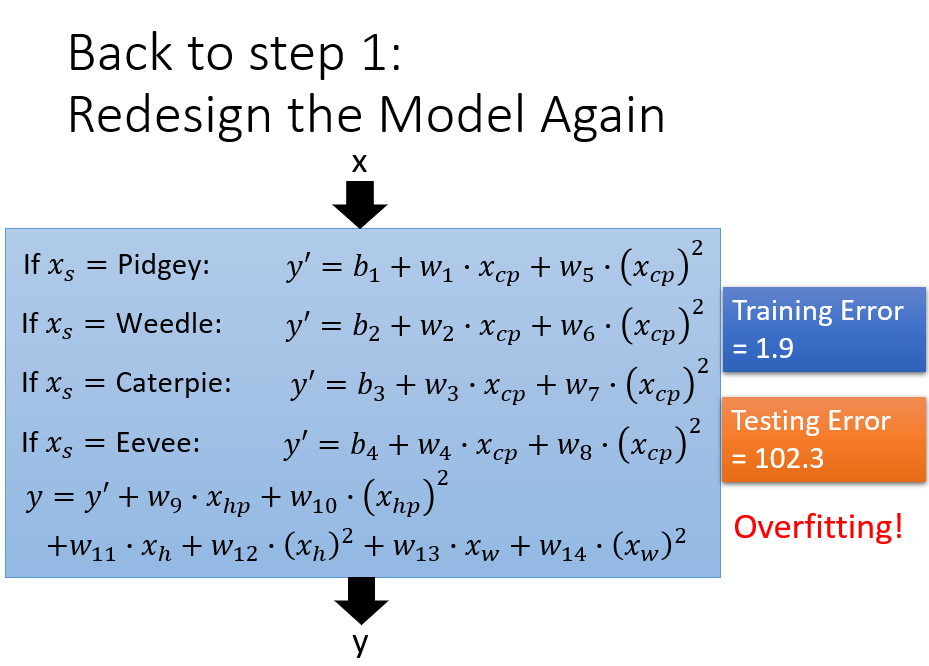
Overfitting
Back to Step 1: Redesign
- x_s = species of x
- 不同物种,不同 w, b
- δ(x_s = )
- = 1, if x_s = Pidgey
- = 0, otherwise
Back to Step 2: Rularization(调整)
不考虑 b
select λ