欠拟合:使用模型的复杂度小于真实模型的复杂度
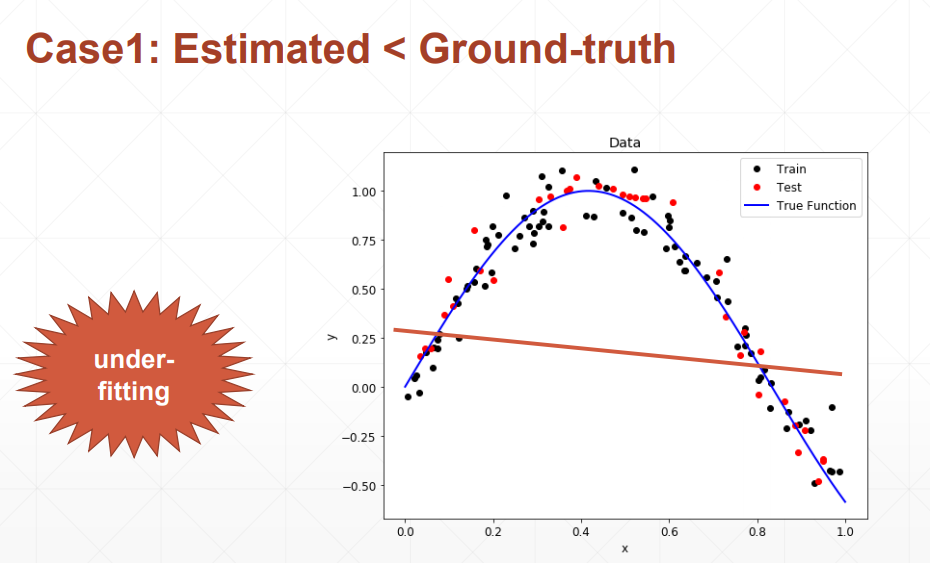
体现在:训练集的loss和准确率都不够理想;测试集的loss和准确率也不理想。
过拟合:使用模型的复杂度大于真实模型的复杂度

体现在:train训练的时候loss和准确率都表现得非常好,但是在测试集上变现得特别不好——泛化能力较差(Generalization Performance)
现实生活中,更多的情况是overfitting。数据集有限,包含了噪声会被模型学习到。
欠拟合:使用模型的复杂度小于真实模型的复杂度

体现在:训练集的loss和准确率都不够理想;测试集的loss和准确率也不理想。
过拟合:使用模型的复杂度大于真实模型的复杂度

体现在:train训练的时候loss和准确率都表现得非常好,但是在测试集上变现得特别不好——泛化能力较差(Generalization Performance)
现实生活中,更多的情况是overfitting。数据集有限,包含了噪声会被模型学习到。
全连接层
nn.Linear(in, out)
简便方法:

Binary Classification
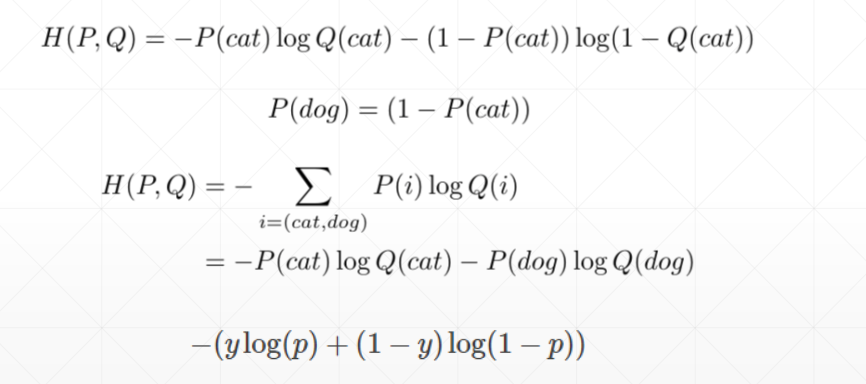
这里的p值是最后的通过激活函数之后的概率值
y是0或1(one—hot编码)

交叉熵从0.916到0.02时,越接近于我们的目标:
是变好的过程
Entropy——熵,指不确定性
熵大则信息量量比较小,越稳定,越没有惊喜度
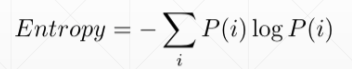
Cross Entropy

Dkl表示的是两个概率分布的距离,当两个概率分布完全相同的时候,距离为0,Dkl=0
当P=Q时:corss Entropy=Entropy
即H(p,q)=H(p)
且在0ne—hot编码规则下H(p)=0, 那我们优化的目标是:
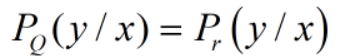
线性回归和逻辑归回/分类问题的区别:
1、函数式不同:
linear regression
y=wx+b;
ligistic regression——在线性回归的基础上加了一个激活函数
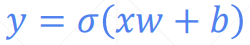
2、目标不同:
线性回顾的目标是预测值接近于真实值;
逻辑回归问题的目标是在x的条件下训练得到y值的概率和当自变量为x时,真实的等于y的概率之间差值最小

无法直接最大化准确率:
准确率的公式为:

分母为所有的y值,分子为预测值等于真实值的个数

(1)存在梯度为0的情况;
计算得到的p=0.4,调整权重之后得到0.45,虽然概率增加了,但是accuray没有发生变化
(2)也有可能存在梯度爆炸的情况
当p值从0.499变动到0.501时,准确的个数增加了一个,当y值(=5)数量较少是,准确个数从3变为4,那么准确率从0.6变动到0.8,准确率变化了0.2,而概率值变动了0.002,则会存在断层连续的情况,也就是梯度爆炸
多类别分类问题——softmax激活函数
2D函数优化实例
反向传播
这里的激活函数统统是sigmoid
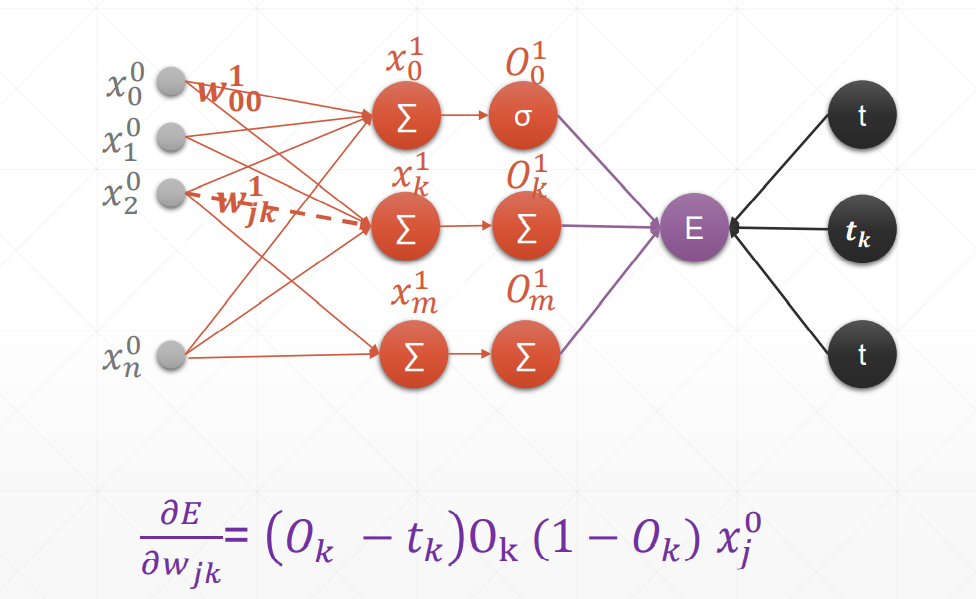
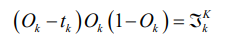
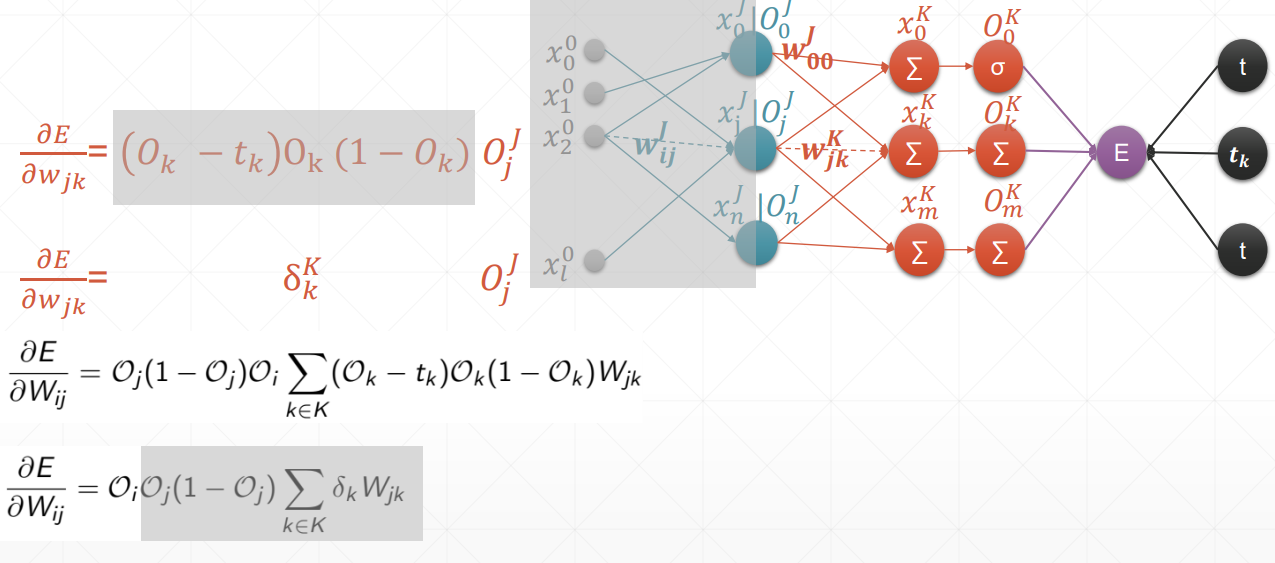
总结:在案例中,oi是输入层,但我们要求得是一个广泛使用的式子,也就是说,在这里我们认为oi是隐藏层。
链式法则
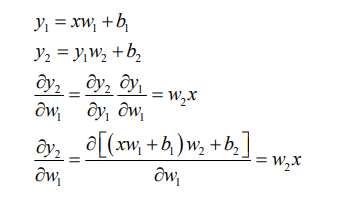
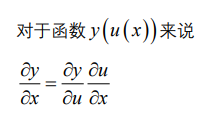

多输出感知机的梯度推导
激活函数仍然是sigmoid,且y的估计函数用到的仍然是一次线性回归函数
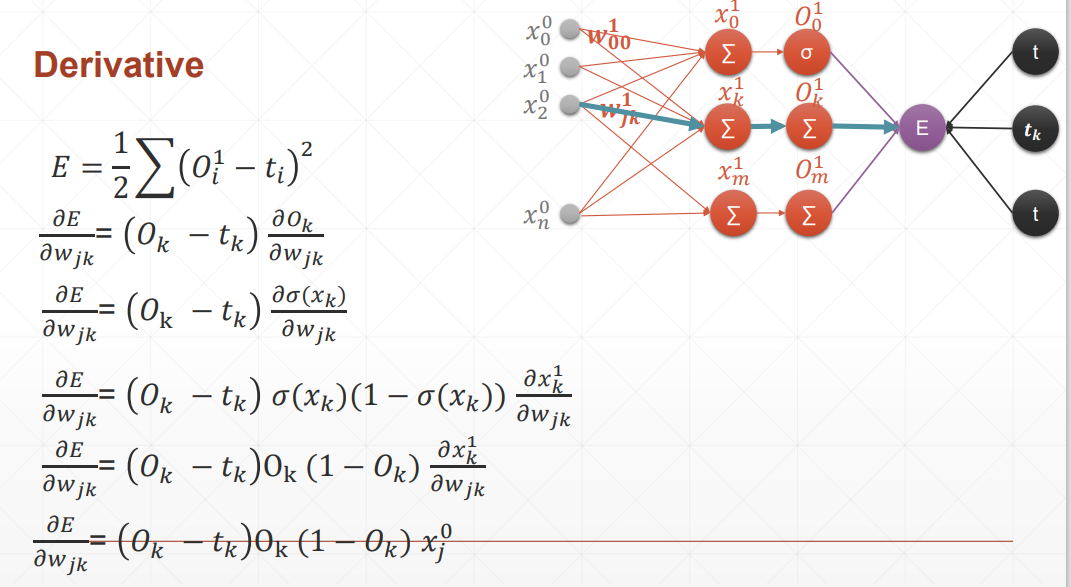
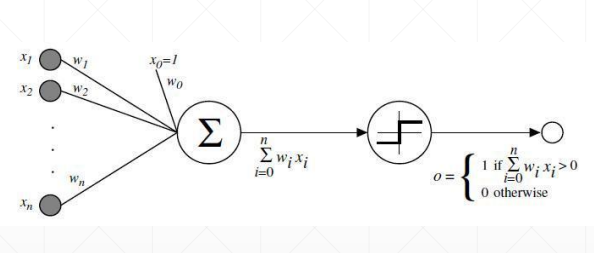
感知机的梯度推导
这里的激活函数是sigmoid激活函数,所以对其求到的结果是,且使用的回归函数是一次线性回归函数。
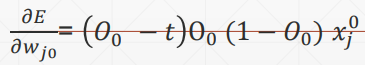
求导
softmax的公式为:
当i=j的时候求导结果为:

当i不等于j的时候求导结果为:

softmax
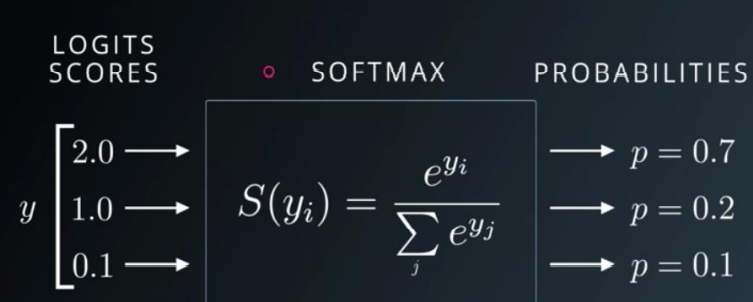
扩大了值之间的差距
Gradient Descent

Gradient:loss损失函数等高线的发现方向
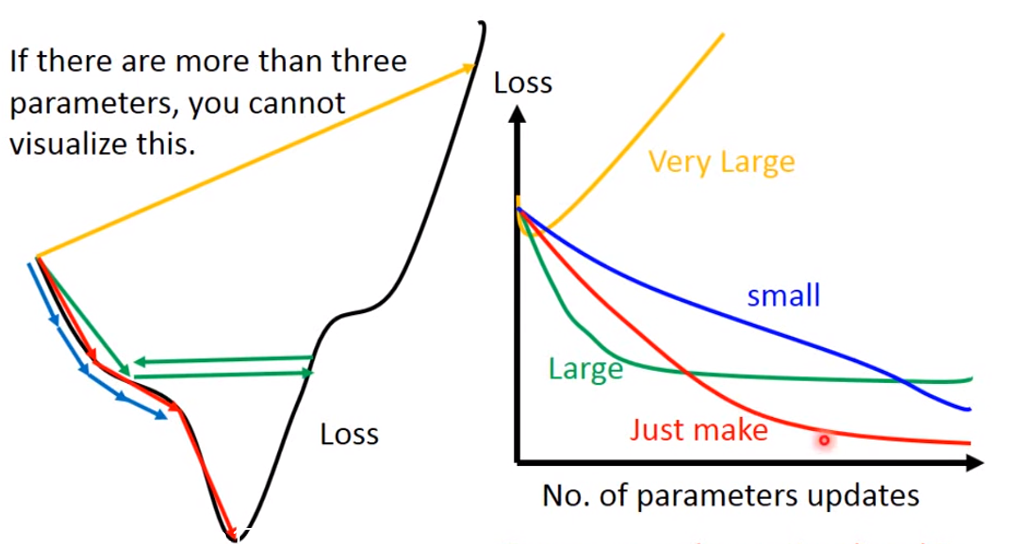
需要注意的是:learning rate 需要设置合理
如果learning rate很小,loss下降的很慢;
如果learning rate表达大,可能卡住,找不到loss的极小值;
如果learning rate非常大,loss有可能越来越大
只有当learning rate 刚刚好的时候,我们才能得到loss的极小值
Adagrad
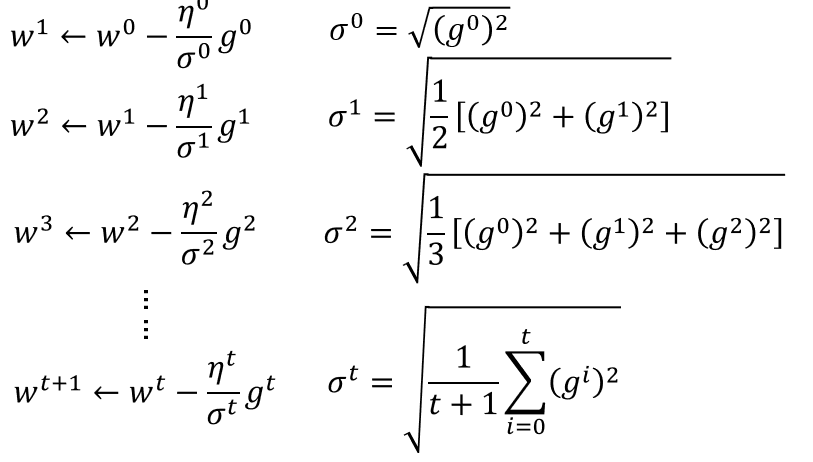
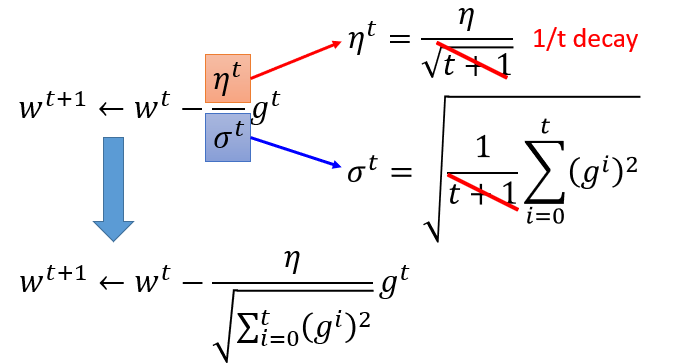
有个矛盾点是,对于gt来说,梯度越大,w参数应该下降得越快,但是分母上也有g的和,分母越大,w参数值下降得越小,这里应该如何理解?

对于2次函数来说,可以直观的看出Adagrad的优势
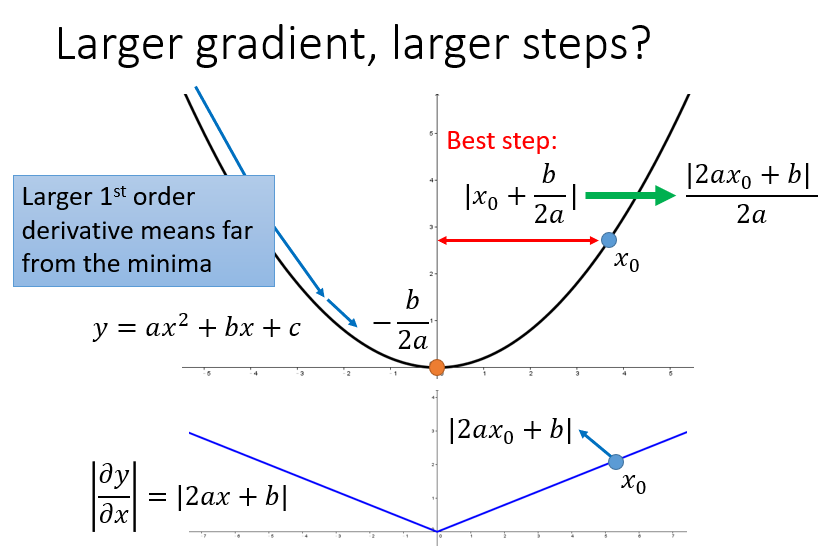
最好的步长是一阶导的绝对值除以二阶导的值
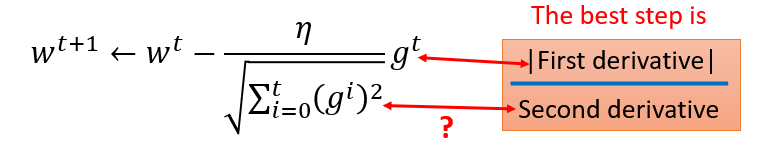
这里的分母虽然是一阶导的绝对值的和,但在一定程度上可以看出二阶导的大小来
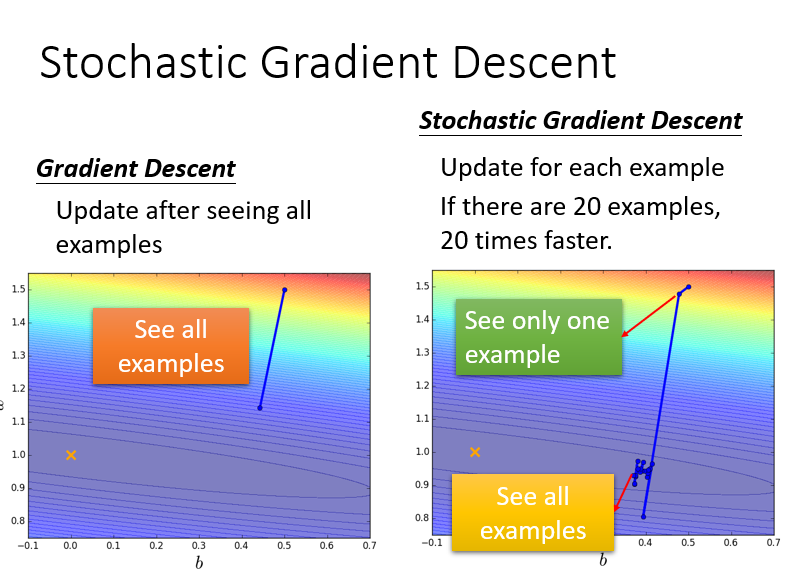
Stochastic Gradient Descent
只看一个example,只考虑一个点的参数值(其实没听懂)
Feature Scaling
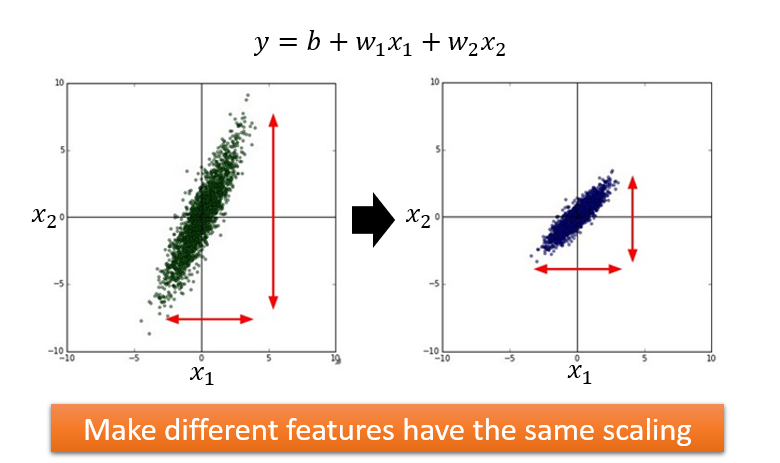
做法:

梯度下降背后的数学原理
泰勒定理:

多元的情况下:

loss及其梯度
典型的loss函数 有:
(1)均方差
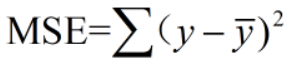
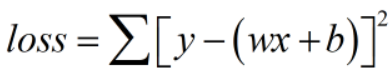
注意:MSE不同于二范数
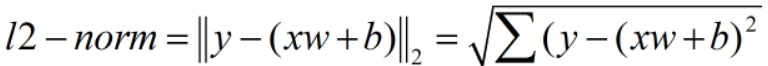
MSE不开根号!
求导
(2)Cross Entropy Loss
可以用于二分类、多分类问题,经常使用softmax激活函数
激活函数及其梯度
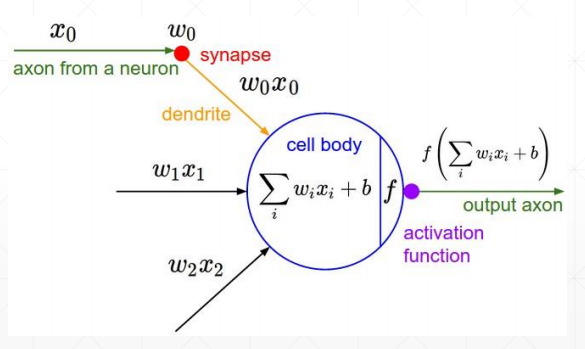
为了解决激活函数不可导的情况,提出了sigmoid/logistic:光滑可导的函数,且把无穷的值域压缩到[0, 1]的范围内

但是会出现梯度离散的情况,参数无法得到更新,因为越往后,导数值与接近于0
sigmoid函数求导之后如下:
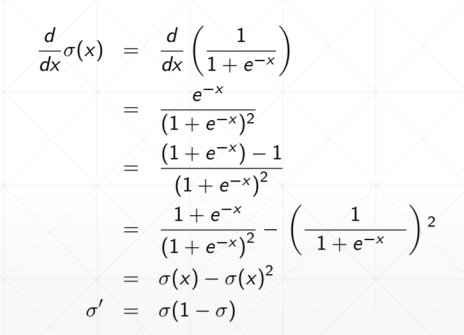
Tanh在RNN里面用得比较多

求导:

Relu使用最多的激活函数
计算导数的时候非常简单,导数为1。不会放大也不会缩小,很大程度上减少了梯度爆炸和梯度离散发生的可能性

递归算法
1.定义递归头
2.递归体
def fact(n):
if n==1:
return n
else:
return n*fact(n-1)
print(fact(5))
import shutil
shutil.make_archive('电影/gg','zip','movie/港台')
import zipfile
z1=zipfile.ZipFile('d:/a.zip','w')
z1.write('1.txt')
z1.write('1_copy.txt')
z.clost()
z2=zipfile.ZipFile('d:/a.zip','r')
z2.extractall('电影')
import shutil
shutil.copyfile('1.txt','1_copy.txt')
shutil.copytree('movie/港台','电影')
import os
path=os.getcwd()
list_files=os.walk(path)
for dirpath,dirnames,filenames in list_files:
for dir in dir names:
print(dir)