可变参数（一个*为元组，**为字典）

强制命名参数（当带星号的“可变参数”后面增加新的参数，必须是强制命名参数）

参数的几种类型

位置参数

默认值参数

命名参数

传递不可变对象：浅拷贝

浅拷贝和深拷贝

浅拷贝：不拷贝子对象的内容，只拷贝子对象的引用。

深拷贝：会连子对象的内存全部拷贝一份，对子对象的修改不会影响源对象。

高效嵌入法embedded

业务选择

说到降维和特征选择，首先要想到的是利用自己的业务能力进行选择，肉眼可见明显和标签有关的特征就是需要留 下的。当然，如果我们并不了解业务，或者有成千上万的特征，那我们也可以使用算法来帮助我们。或者，可以让 算法先帮助我们筛选过一遍特征，然后在少量的特征中，我们再根据业务常识来选择更少量的特征。

PCA和SVD一般不用

逻辑回归是由线性回归演变而来，线性回归的一个核心目的是通过求解参数来探究特征X与标签y之间的 关系，而逻辑回归也传承了这个性质，我们常常希望通过逻辑回归的结果，来判断什么样的特征与分类结果相关， 因此我们希望保留特征的原貌。PCA和SVD的降维结果是不可解释的，因此一旦降维后，我们就无法解释特征和标 签之间的关系了。当然，在不需要探究特征与标签之间关系的线性数据上，降维算法PCA和SVD也是可以使用的。

统计方法可以使用，但不是非常必要

逻辑回归对数据的要求低于线性回归，由于我们不是使用最小二乘法来求解，所以逻辑回归对数据的总体分布和方差没有要求，也不需要排除特征之间的共线性，但如果我 们确实希望使用一些统计方法，比如方差，卡方，互信息等方法来做特征选择，也并没有问题。过滤法中所有的方法，都可以用在逻辑回归上。

重要参数penatly&C

1、正则化

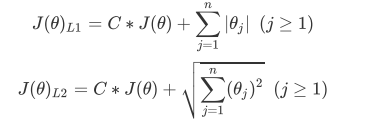
L1正则化和L2正则化虽然都可以控制过拟合，但它们的效果并不相同。当正则化强度逐渐增大（即C逐渐变小）， 参数的取值会逐渐变小，但L1正则化会将参数压缩为0，L2正则化只会让参数尽量小，不会取到0。

在L1正则化在逐渐加强的过程中，携带信息量小的、对模型贡献不大的特征的参数，会比携带大量信息的、对模型 有巨大贡献的特征的参数更快地变成0，所以L1正则化本质是一个特征选择的过程，掌管了参数的“稀疏性”。L1正 则化越强，参数向量中就越多的参数为0，参数就越稀疏，选出来的特征就越少，以此来防止过拟合。

相对的，L2正则化在加强的过程中，会尽量让每个特征对模型都有一些小的贡献，但携带信息少，对模型贡献不大 的特征的参数会非常接近于0。通常来说，如果我们的主要目的只是为了防止过拟合，选择L2正则化就足够了。但 是如果选择L2正则化后还是过拟合，模型在未知数据集上的效果表现很差，就可以考虑L1正则化。

为什么需要逻辑回归

1. 逻辑回归对线性关系的拟合效果好到丧心病狂，特征与标签之间的线性关系极强的数据，比如金融领域中的 信用卡欺诈，评分卡制作，电商中的营销预测等等相关的数据，都是逻辑回归的强项。虽然现在有了梯度提 升树GDBT，比逻辑回归效果更好，也被许多数据咨询公司启用，但逻辑回归在金融领域，尤其是银行业中的 统治地位依然不可动摇（相对的，逻辑回归在非线性数据的效果很多时候比瞎猜还不如，所以如果你已经知 道数据之间的联系是非线性的，千万不要迷信逻辑回归）；

2. 逻辑回归计算快：对于线性数据，逻辑回归的拟合和计算都非常快，计算效率优于SVM和随机森林，亲测表示在大型数据上尤其能够看得出区别；

3. 逻辑回归返回的分类结果不是固定的0，1，而是以小数形式呈现的类概率数字：我们因此可以把逻辑回归返 回的结果当成连续型数据来利用。比如在评分卡制作时，我们不仅需要判断客户是否会违约，还需要给出确 定的”信用分“，而这个信用分的计算就需要使用类概率计算出的对数几率，而决策树和随机森林这样的分类 器，可以产出分类结果，却无法帮助我们计算分数（当然，在sklearn中，决策树也可以产生概率，使用接口 predict_proba调用就好，但一般来说，正常的决策树没有这个功能）。

另外，逻辑回归还有抗噪能力强的优点。福布斯杂志在讨论逻辑回归的优点时，甚至有着“技术上来说，最佳模型 的AUC面积低于0.8时，逻辑回归非常明显优于树模型”的说法。并且，逻辑回归在小数据集上表现更好，在大型的 数据集上，树模型有着更好的表现。

由此，我们已经了解了逻辑回归的本质，它是一个返回对数几率的，在线性数据上表现优异的分类器，它主要被应 用在金融领域。其数学目的是求解能够让模型对数据拟合程度最高的参数 的值，以此构建预测函数 ，然后将 特征矩阵输入预测函数来计算出逻辑回归的结果y。注意，虽然我们熟悉的逻辑回归通常被用于处理二分类问题， 但逻辑回归也可以做多分类。

重要接口inverse_transform

神奇的接口inverse_transform，可以将我们归一化，标准化，甚至做过哑变 量的特征矩阵还原回原始数据中的特征矩阵，这几乎在向我们暗示，任何有inverse_transform这个接口的过程都 是可逆的。PCA应该也是如此。

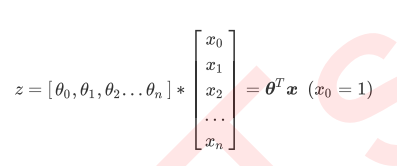
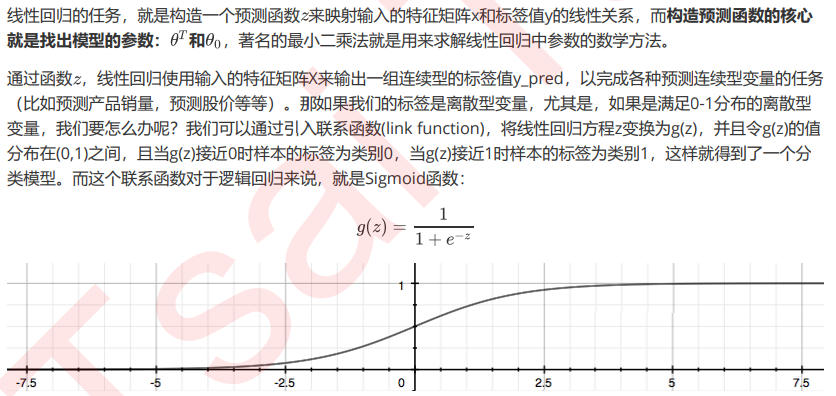
而逻辑回归，是一种名为“回归”的线性分类器，其本质是由线性回 归变化而来的，一种广泛使用于分类问题中的广义回归算法。要理解逻辑回归从何而来，得要先理解线性回归。线 性回归是机器学习中最简单的的回归算法，它写作一个几乎人人熟悉的方程：

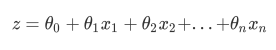
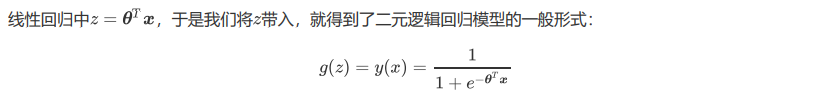
传递不可变对象

不可变对象：int、float、字符串、元组、布尔值

在赋值操作时会创建一个对象。

参数的传递：从实参到形参的赋值操作。

所有的赋值操作都是”引用的赋值“,Python中参数的传递都是“引用传递”，不是“值传递”。

可变对象：字典、列表、集合、自定义的对象

局部变量和全局变量效率测试

局部变量的查询和访问速度比全局变量快，优先考虑局部变量。

变量的作用域（全局变量和局部变量）

全局变量：作用域为定义的模块。（少定义）（作为常量）（函数内部想改变全局变量的值，使用global声明一下）

局部变量：作用域为函数体。在栈的栈帧中，调用完函数就删除。

函数也是对象，内存底层分析

对象：堆里面的内存块

def:在堆里创建函数对象

同时在栈里创建对象名字是函数名称，值为函数地址，进行调用时，函数名称（），表示调用函数，顺着地址找到函数进行调用，创建一次调用多次，

特征选择：方差过滤

```python
from sklearn.feature_selection import VarianceThreshold #特征选择，根据方差进行过滤
def var():
    '''
    特征选择-选择低方差的特征
    :return:None
    '''
    var=VarianceThreshold(threshold=1.0)#保留方差值为1的数值
    data=var.fit_transform([[0,2,0,3],[0,1,4,3],[0,1,1,3]])#三行四列的二维数组
    print(data)
    return None

if __name__=='__main__':  #调用
 var()
```

PCA:主成分分析   

把维度降低，但是数据信息尽可能不损耗

形参和实参

文档字符串（函数的注释）

函数用法和底层分析

函数是可重用的程序代码块。python中，定义函数的语法如下：

def 函数名（[参数列表]）：

      '''文档字符串'''

      函数体/若干语句

要点：

       使用def来定义函数，def之后是空格，然后是函数名和()，Python执行def时，会创建一个函数对象，并绑定到函数名变量上。

推导式创建序列

列表推导式

列表推导式生成列表对象，语法如下：

    [表达式  for   item   in    可迭代对象]

字典推导式

    {key:value  for  value  for  表达式  in  可迭代对象}

集合推导式

    {表达式 for  item   in  可迭代对象}

生成器推导式（用于生成元组）

一个生成器只能运行一次，用过不可再用。