处理连续型特征:二值化和分箱
根据阈值将数据二值化(将特征值设置为0或1),用于处理连续型变量。大于阈值的值映射为1,而小于或等于阈 值的值映射为0。默认阈值为0时,特征中所有的正值都映射到1。
二值化是对文本计数数据的常见操作,分析人员 可以决定仅考虑某种现象的存在与否。它还可以用作考虑布尔随机变量的估计器的预处理步骤(例如,使用贝叶斯 设置中的伯努利分布建模)。
分箱

处理连续型特征:二值化和分箱
根据阈值将数据二值化(将特征值设置为0或1),用于处理连续型变量。大于阈值的值映射为1,而小于或等于阈 值的值映射为0。默认阈值为0时,特征中所有的正值都映射到1。
二值化是对文本计数数据的常见操作,分析人员 可以决定仅考虑某种现象的存在与否。它还可以用作考虑布尔随机变量的估计器的预处理步骤(例如,使用贝叶斯 设置中的伯努利分布建模)。
分箱

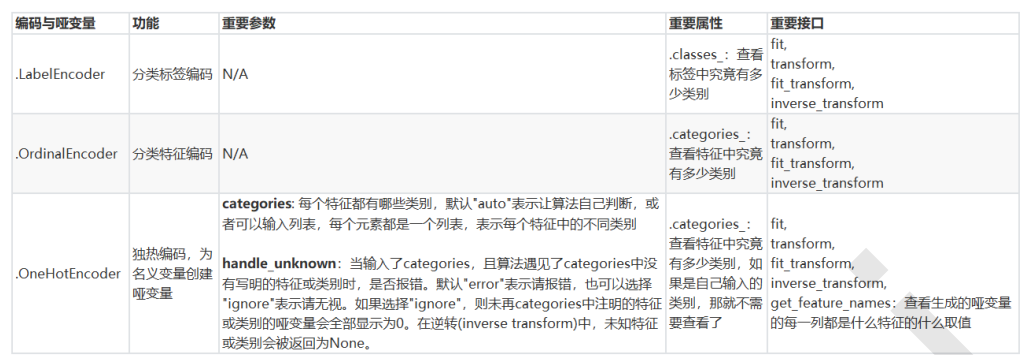
处理分类型特征:编码与哑变量
LabelEncoder:标签专用,能够将分类转换为分类数值
OrdinalEncoder:特征专用,能够将分类特征转换为分类数值
OneHotEncoder:独热编码,创建哑变量
类别OrdinalEncoder可以用来处理有序变量,但对于名义变量,我们只有使用哑变量的方式来处理,才能够尽量向算法传达最准确的信息:
缺失值
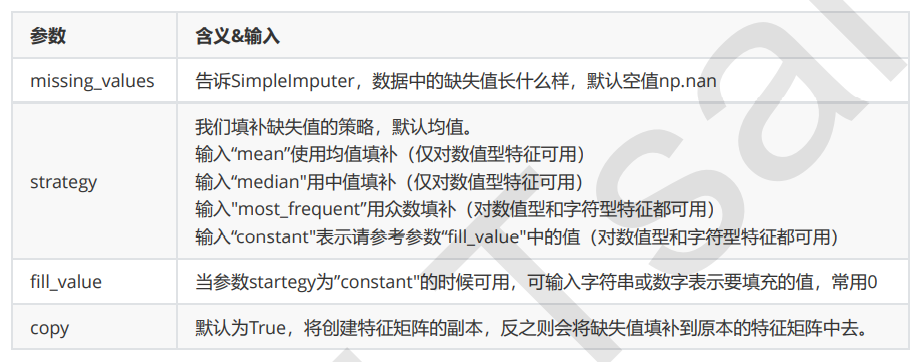
impute.SimpleImputer
StandardScaler
当数据(x)按均值(μ)中心化后,再按标准差(σ)缩放,数据就会服从为均值为0,方差为1的正态分布(即标准正态分 布),而这个过程,就叫做数据标准化(Standardization,又称Z-score normalization),公式如下:
对于StandardScaler和MinMaxScaler来说,空值NaN会被当做是缺失值,在fit的时候忽略,在transform的时候 保持缺失NaN的状态显示。
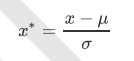
并且,尽管去量纲化过程不是具体的算法,但在fit接口中,依然只允许导入至少二维数 组,一维数组导入会报错。通常来说,我们输入的X会是我们的特征矩阵,现实案例中特征矩阵不太可能是一维所以不会存在这个问题。
StandardScaler和MinMaxScaler选哪个?
大多数机器学习算法中,会选StandardScaler来进行特征缩放,因为MinMaxScaler对异常值非常敏感。

数据无量纲化
在机器学习算法实践中,我们往往有着将不同规格的数据转换到同一规格,或不同分布的数据转换到某个特定分布 的需求,这种需求统称为将数据“无量纲化”。
数据的无量纲化可以是线性的,也可以是非线性的。线性的无量纲化包括中心化(Zero-centered或者Meansubtraction)处理和缩放处理(Scale)。中心化的本质是让所有记录减去一个固定值,即让数据样本数据平移到 某个位置。
preprocessing.MinMaxScaler
当数据(x)按照最小值中心化后,再按极差(最大值 - 最小值)缩放,数据移动了最小值个单位,并且会被收敛到 [0,1]之间,而这个过程,就叫做数据归一化(Normalization,又称Min-Max Scaling)。注意,Normalization是归 一化,不是正则化,真正的正则化是regularization,不是数据预处理的一种手段。归一化之后的数据服从正态分 布,公式如下:
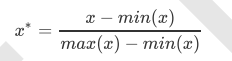
在sklearn当中,我们使用preprocessing.MinMaxScaler来实现这个功能。MinMaxScaler有一个重要参数, feature_range,控制我们希望把数据压缩到的范围,默认是[0,1]。
axis = 0 按行计算,得到列的性质。
axis = 1 按列计算,得到行的性质。
特征工程
数据挖掘的五大流程:
1. 获取数据
2. 数据预处理 数据预处理是从数据中检测,纠正或删除损坏,不准确或不适用于模型的记录的过程 可能面对的问题有:数据类型不同,比如有的是文字,有的是数字,有的含时间序列,有的连续,有的间断。 也可能,数据的质量不行,有噪声,有异常,有缺失,数据出错,量纲不一,有重复,数据是偏态,数据量太 大或太小 数据预处理的目的:让数据适应模型,匹配模型的需求
3. 特征工程: 特征工程是将原始数据转换为更能代表预测模型的潜在问题的特征的过程,可以通过挑选最相关的特征,提取 特征以及创造特征来实现。其中创造特征又经常以降维算法的方式实现。 可能面对的问题有:特征之间有相关性,特征和标签无关,特征太多或太小,或者干脆就无法表现出应有的数 据现象或无法展示数据的真实面貌 特征工程的目的:1) 降低计算成本,2) 提升模型上限
4. 建模,测试模型并预测出结果
5. 上线,验证模型效果
1.2 sklearn中的数据预处理和特征工程
模块preprocessing:几乎包含数据预处理的所有内容
模块Impute:填补缺失值专用
模块feature_selection:包含特征选择的各种方法的实践
模块decomposition:包含降维算法
列表元素的增加和删除
append()方法:在列表尾部直接加元素
a=[10,20]
a.append('wo')
print(a) #[10, 20, 'wo']
a=[10,20,30] a.append([12,14]) print(a) #[10, 20, 30, [12, 14]] a.append(15,17) print(a) #错误,append只能添加一个元素
+运算符操作:创建新的列表对象,将原来的列表元素复制到新的列表对象中。(不建议)
a=[10,20] print(id(a)) a=a+[3,4] #2568250519936 print(a) #[10, 20, 3, 4] print(id(a)) #2568245607744重新生成了列表
extend():原地操作,不创建新的列表对象
a=[10,20,30] print(id(a)) #2043085779328 a.extend([2,4]) print(a) #[10, 20, 30, 2, 4] print(id(a)) #2043085779328没有生成新的对象
insert():可以将指定元素插入到列表对象的指定位置。(不建议)
a=[10,20,30] a.insert(2,100) print(a) #[10, 20, 100, 30]
乘法扩展
a=[10]*3 print(a) #[10, 10, 10]
列表的创建
基本语法的创建
a=[20,30,50,'xiaohong'] print(a[0]) #20 b=[] b.append(10) print(b) #[10]
list()创建:list()将任何可以迭代的数据转化为列表。
a=list('fuzhuoming')
print(a) #['f', 'u', 'z', 'h', 'u', 'o', 'm', 'i', 'n', 'g']
b=list(range(5))
print(b) #[0, 1, 2, 3, 4]
range()创建整数列表
range[start,end,step]
c=list(range(0,10,2)) print(c) #[0, 2, 4, 6, 8]range()完整用法
推到式生成列表
序列:一种数据储存方式,用来储存一系列的数据。在内存中,序列就是一块用来存放多个值(对象的地址)的连续的内存空间。
常用的序列结构:字符串、列表、元组、字典、集合。
列表:用于存储任意数目,任意类型的数据集合。
列表大小可变。字符串和列表都是序列lei'xi
基本运算符
and、or、not布尔与或非
is、is not判断是否为同一个对象
<、>比较值是否相等
a=4 print(3<a<10) #True 关系运算符可以连用
字符串常用方法汇总
(1)常用查找方法
用来衡量模型在未知数据上的准确率的指标,叫做泛化误差(Genelization error)
泛化误差:
当模型在未知数据(测试集或者袋外数据)上表现糟糕时,我们说模型的泛化程度不够,泛化误差大,模型的效果 不好。泛化误差受到模型的结构(复杂度)影响。看下面这张图,它准确地描绘了泛化误差与模型复杂度的关系, 当模型太复杂,模型就会过拟合,泛化能力就不够,所以泛化误差大。当模型太简单,模型就会欠拟合,拟合能力 就不够,所以误差也会大。只有当模型的复杂度刚刚好的才能够达到泛化误差最小的目标。
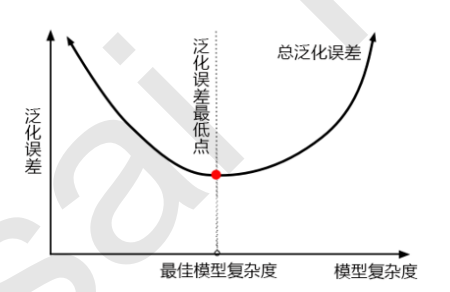
1)模型太复杂或者太简单,都会让泛化误差高,我们追求的是位于中间的平衡点
2)模型太复杂就会过拟合,模型太简单就会欠拟合
3)对树模型和树的集成模型来说,树的深度越深,枝叶越多,模型越复杂
4)树模型和树的集成模型的目标,都是减少模型复杂度,把模型往图像的左边移动

可变字符串
在Python中,字符串属于不可变对象,如果需要修改其中的值,只能创建新的字符串对象。但是可以用io.StringIO对象或array模块。
字符串的格式化
format():通过{索引}/{参数名}直接映射参数值,实现对字符串的格式化。
填充与对齐
数字格式化
实例:用随机森林回归填补缺失值
我们从现实中收集的数据,几乎不可能是完美无缺的,往往都会有一些缺失值。面对缺失值,很多人选择的方式是 直接将含有缺失值的样本删除,这是一种有效的方法,但是有时候填补缺失值会比直接丢弃样本效果更好,即便我 们其实并不知道缺失值的真实样貌。我们可以使用sklearn.impute.SimpleImputer来轻松地将均 值,中值,或者其他最常用的数值填补到数据中
随机森林回归器
重要参数,属性与接口
criterion
回归树衡量分枝质量的指标,支持的标准有三种: 1)输入"mse"使用均方误差mean squared error(MSE),父节点和叶子节点之间的均方误差的差额将被用来作为 特征选择的标准,这种方法通过使用叶子节点的均值来最小化L2损失
2)输入“friedman_mse”使用费尔德曼均方误差,这种指标使用弗里德曼针对潜在分枝中的问题改进后的均方误差
3)输入"mae"使用绝对平均误差MAE(mean absolute error),这种指标使用叶节点的中值来最小化L1损失
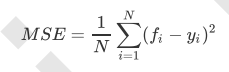
在回归中,我们追求的是,MSE越小越好。 然而,回归树的接口score返回的是R平方,并不是MSE。R平方被定义如下:
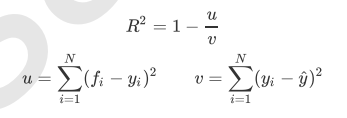
虽然均方误差永远为正,但是sklearn当中使用均方误差作为评判标准时,却是计算”负均方误 差“(neg_mean_squared_error)。
最重要的属性和接口,都与随机森林的分类器相一致,还是apply, fit, predict和score最为核心。值得一提的是,随 机森林回归并没有predict_proba这个接口,因为对于回归来说,并不存在一个样本要被分到某个类别的概率问 题,因此没有predict_proba这个接口。
Bonus:Bagging的另一个必要条件
有另一个必要条件:基分类器的判断准 确率至少要超过随机分类器,即基分类器的判断准确率至少要超过50%。
可以从图像上看出,当基分类器的误差率小于0.5,即准确率大于0.5时,集成的效果是比基分类器要好的。相反, 当基分类器的误差率大于0.5,袋装的集成算法就失效了。所以在使用随机森林之前,一定要检查,用来组成随机 森林的分类树们是否都有至少50%的预测正确率。率至少要超过50%。
随机森林的本质是一种装袋集成算法(bagging),装袋集成算法是对基评估器的预测结果进行平均或用多数表决 原则来决定集成评估器的结果。在刚才的红酒例子中,我们建立了25棵树,对任何一个样本而言,平均或多数表决 原则下,当且仅当有13棵以上的树判断错误的时候,随机森林才会判断错误。单独一棵决策树对红酒数据集的分类 准确率在0.85上下浮动,假设一棵树判断错误的可能性为0.2(ε)。所以,当一共有25棵树时,判断错误的可能性为:
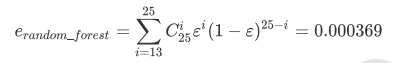
可见,判断错误的几率非常小,这让随机森林在红酒数据集上的表现远远好于单棵决策树。
随机森林中其实也有random_state,用法和分类树中相似,只不过在分类树中,一个random_state只控制生成一 棵树,而随机森林中的random_state控制的是生成森林的模式,而非让一个森林中只有一棵树。
当random_state固定时,随机森林中生成是一组固定的树,但每棵树依然是不一致的,这是 用”随机挑选特征进行分枝“的方法得到的随机性。并且我们可以证明,当这种随机性越大的时候,袋装法的效果一 般会越来越好。用袋装法集成时,基分类器应当是相互独立的,是不相同的。
bootstrap & oob_score
要让基分类器尽量都不一样,一种很容易理解的方法是使用不同的训练集来进行训练,而袋装法正是通过有放回的随机抽样技术来形成不同的训练数据,bootstrap就是用来控制抽样技术的参数。
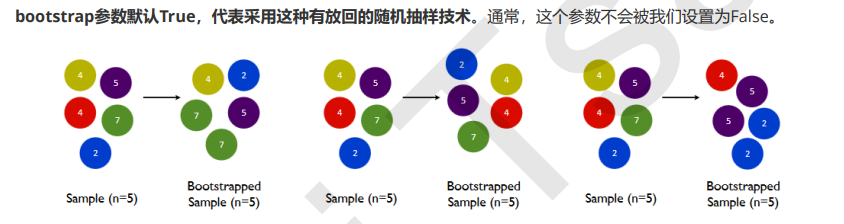
一般来说,自助集大约平均会包含63%的原始数据。因为每一个样本被抽到某个自助集中的概率为:
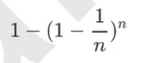
当n足够大时,这个概率收敛于1-(1/e),约等于0.632。因此,会有约37%的训练数据被浪费掉,没有参与建模, 这些数据被称为袋外数据(out of bag data,简写为oob)。
也就是说,在使用随机森林时,我们可以不划分测试集和训练集,只需要用袋外 数据来测试我们的模型即可。
重要属性和接口
控制基评估器

单个决策树的准确率越高,随机森林的准确率也会越高,因为装袋法是依赖于平均值或 者少数服从多数原则来决定集成的结果的。
n_estimators
n_estimators越 大,模型的效果往往越好。但是相应的,任何模型都有决策边界,n_estimators达到一定的程度之后,随机森林的 精确性往往不在上升或开始波动,并且,n_estimators越大,需要的计算量和内存也越大,训练的时间也会越来越 长。对于这个参数,我们是渴望在训练难度和模型效果之间取得平衡。
n_estimators的默认值在现有版本的sklearn中是10,但是在即将更新的0.22版本中,这个默认值会被修正为 100。这个修正显示出了使用者的调参倾向:要更大的n_estimators。
实操:建一片森林
随机森林
集成算法概述
集成学习(ensemble learning)是时下非常流行的机器学习算法,它本身不是一个单独的机器学习算法,而是通 过在数据上构建多个模型,集成所有模型的建模结果。基本上所有的机器学习领域都可以看到集成学习的身影,在 现实中集成学习也有相当大的作用,它可以用来做市场营销模拟的建模,统计客户来源,保留和流失,也可用来预 测疾病的风险和病患者的易感性。在现在的各种算法竞赛中,随机森林,梯度提升树(GBDT),Xgboost等集成 算法的身影也随处可见,可见其效果之好,应用之广。
多个模型集成成为的模型叫做集成评估器(ensemble estimator),组成集成评估器的每个模型都叫做基评估器 (base estimator)。通常来说,有三类集成算法:装袋法(Bagging),提升法(Boosting)和stacking。
装袋法的核心思想是构建多个相互独立的评估器,然后对其预测进行平均或多数表决原则来决定集成评估器的结 果。装袋法的代表模型就是随机森林。
提升法中,基评估器是相关的,是按顺序一一构建的。其核心思想是结合弱评估器的力量一次次对难以评估的样本 进行预测,从而构成一个强评估器。提升法的代表模型有Adaboost和梯度提升树。
