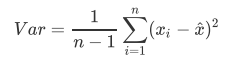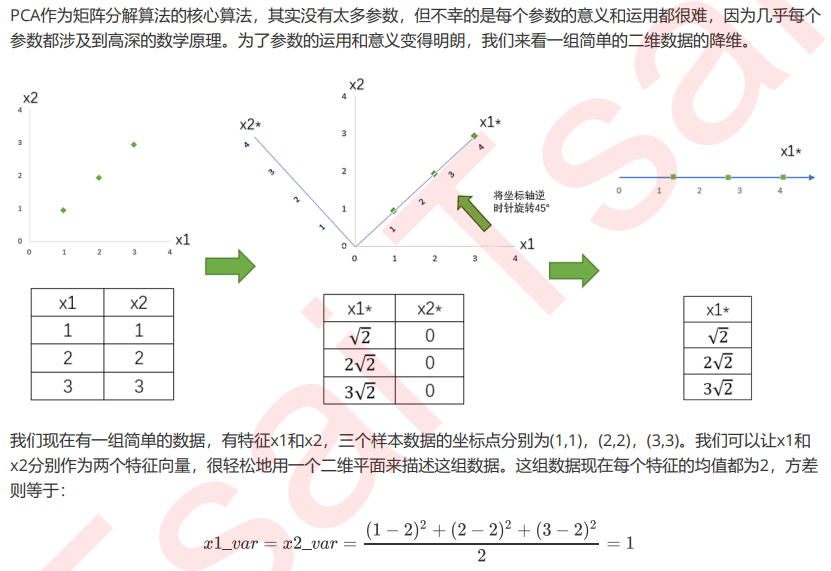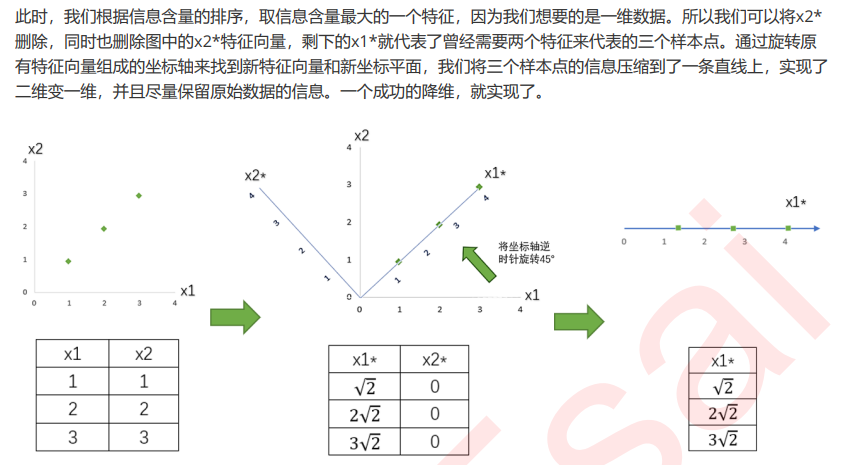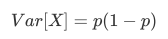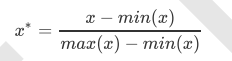
选取超参数threshold
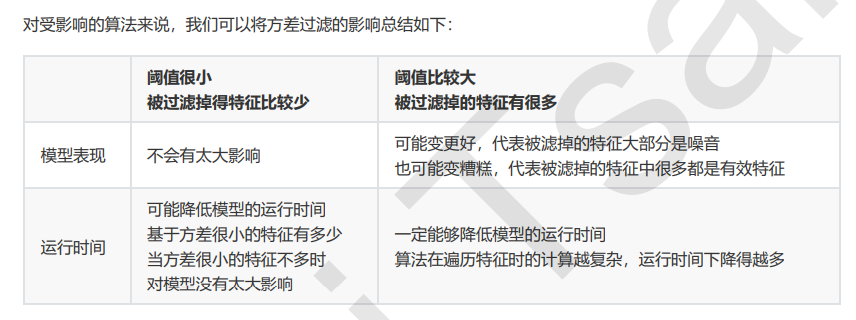
我们怎样知道,方差过滤掉的到底时噪音还是有效特征呢?过滤后模型到底会变好还是会变坏呢?答案是:每个数据集不一样,只能自己去尝试。这里的方差阈值,其实相当于是一个超参数,要选定最优的超参数,我们可以画学 习曲线,找模型效果最好的点。但现实中,我们往往不会这样去做,因为这样会耗费大量的时间。我们只会使用阈值为0或者阈值很小的方差过滤,来为我们优先消除一些明显用不到的特征,然后我们会选择更优的特征选择方法 继续削减特征数量。
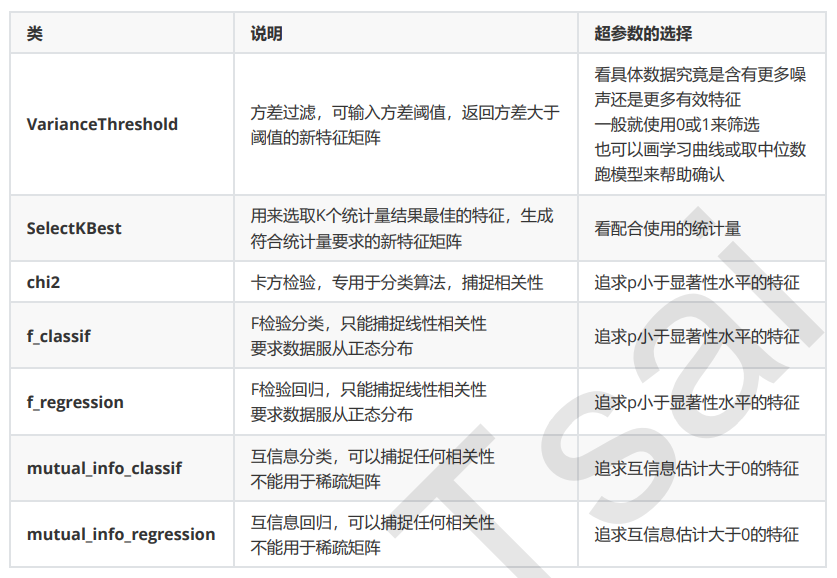
方差挑选完毕之后,我们就要考虑下一个问题:相关性了。我们希望选出与标签相关且有意义的特征,因为这样的特征能够为我们提供大量信息。如果特征与标签无关,那只会白白浪费我们的计算内存,可能还会给模型带来噪 音。在sklearn当中,我们有三种常用的方法来评判特征与标签之间的相关性:卡方,F检验,互信息。
卡方过滤是专门针对离散型标签(即分类问题)的相关性过滤。卡方检验类feature_selection.chi2计算每个非负 特征和标签之间的卡方统计量,并依照卡方统计量由高到低为特征排名。再结合feature_selection.SelectKBest 这个可以输入”评分标准“来选出前K个分数最高的特征的类,我们可以借此除去最可能独立于标签,与我们分类目 的无关的特征。
如果卡方检验检测到某个特征中所有的值都相同,会提示我们使用方差先进行方差过滤。并且,刚才我们已 经验证过,当我们使用方差过滤筛选掉一半的特征后,模型的表现时提升的。因此在这里,我们使用threshold=中 位数时完成的方差过滤的数据来做卡方检验。
卡方检验的本质是推测两组数据之间的差异,其检验的原假设是”两组数据是相互独立的”。卡方检验返回卡方值和 P值两个统计量,其中卡方值很难界定有效的范围,而p值,我们一般使用0.01或0.05作为显著性水平,即p值判断 的边界,具体我们可以这样来看: