索引与切片

4、rand、rand_like、randint

rand随机生成在[0, 1]的数值

rand_like是先把rand生成的数组读取出来再喂给rand函数

randint需要给出最大值、最小值和shape

创建tensor

（1）从numpy进行导入

（2）从list里面导入

小写的tensor括号里接收的是现有数据，而大写Terson、FloatTensor里面接受的是形状，也可以接受现成的数据，括号里用中括号时表示现成的数据，括号时输入的形状

Dim1

一般会用在bias、线性层的输入

Dim2

一般用在batch，当输入多张图片时，第一个数字是图片的个数，第二个是打平图片之后的一维点数

Dim3

适合RNN的文字处理

Dim4

适合CNN

第一个数字是图片的个数，第二个数字是图片的通道，通道为1是灰色图像，通道为3的是菜色图像，后两位数字28*28是minis数据集的长和宽

pytorch中的数据类型

没有对string的支持内键

how to denote string

（1）One-hot并不体现语义

（2）Embedding—word2vec

核实数据类型

数据类型

（1）标量

回归问题实战

（1）先计算总损失值

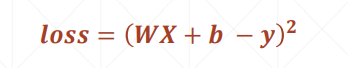
（2）然后计算w和b的偏导，进而更新梯度值

需要四步：
（1）load data

（2）build model

（3）train

（4）test

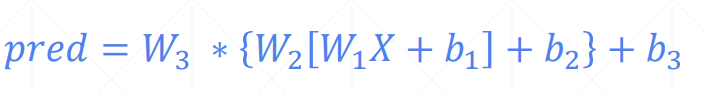
Non-linear Factor

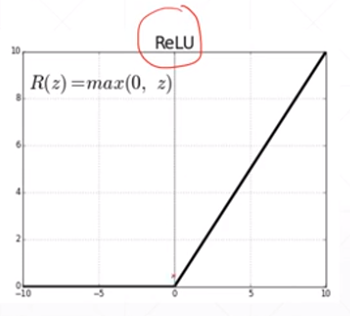
加入激活函数之后

pred既有线性表达能力，还有非线性的表达能力

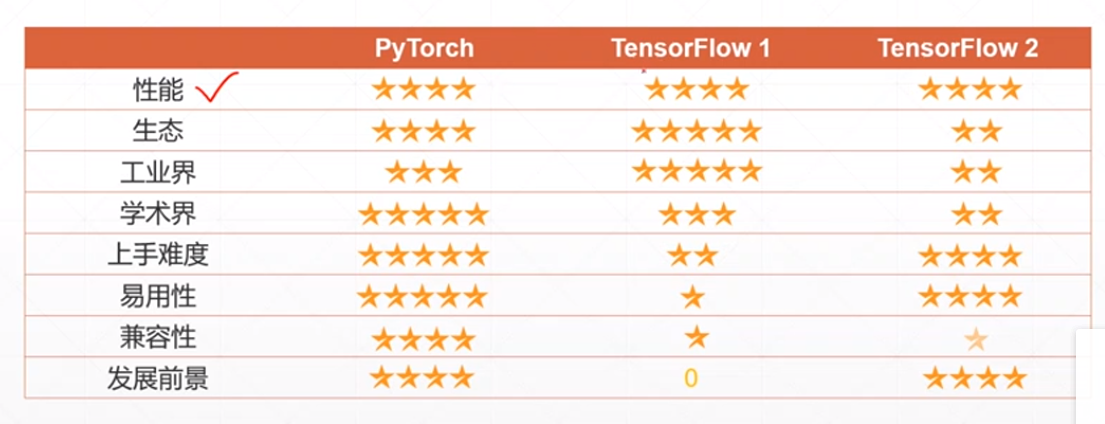
pytorch的功能：
（1）CPU加速；

没有显卡，用不了cuda

（2）自动求导*非常重要，因为深度学习本质上就是在利用梯度下降法来求最优解；

（3）常用网络层

静态图：

define——>run

在最开始就需要定义好公式，给定输入值，得到输出值，而且在运行的过程中无法进行调整

动态图：

可以随时调整公式

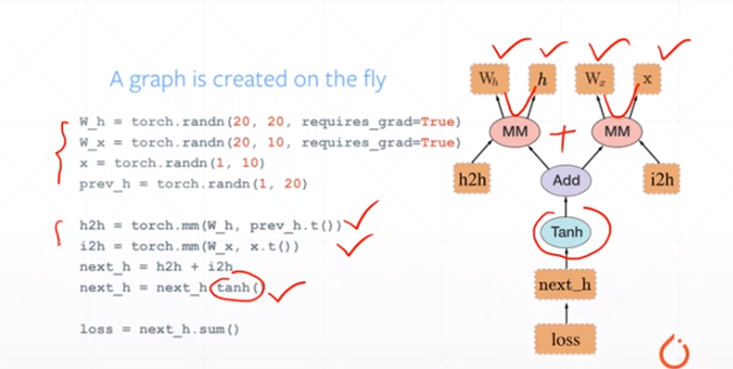
linear Regression——我们要估计连续函数的值；

logistic Regression——在上述linear regression的基础上增加了一个激活函数，把y的空间压缩到0-1的范围，0-1可以表示一个概率

classification——所有的可能性概率之和为1

梯度下降法

模型选择：了解每个模型；

EM算法无监督聚类燕尾花

GMM与图片分析

图像卷积

crawler 爬数据

### 对于LightGBM：又轻又快

在不降低准确率的前提下，速度提升了10倍左右，占用内存下降了3倍左右。因为它是基于决策树算法的，它采用最优的==叶明智==策略分裂叶子节点，然而它的提升算法分裂树一般采用的是深度方向或者水平明智。因此，当增长到相同的叶子节点，叶明智算法比水平-wise算法减少更多得损失。因此导致更高的精度。

J_\theta=-l(\theta)

### logistic函数：通过回归进行分类

### logistic回归的过程

- 1) 找到一个合适的预测函数，一般表示为h函数，该函数就是我们需要找的分类函数，它用来预测输入数据的判断结果。这个过程是非常关键的，需要对数据有一定的了解和分析，知道或者猜测预测函数的大概形式，比如是线性函数还是非线性函数。

- 2）构造一个loss损失函数，该函数表示预测的输出与训练数据类别之间的偏差。可以是二者之间的差或者是其他的形式。综合考虑所有训练数据的损失，将loss求和或者求平均，记为J(theta)函数，表示所有训练数据预测值与实际类别的偏差。

- 3）显然，J函数的值越小表示预测函数越准确。所以这一步需要做的是找到J函数的最小值。找到最小值有不同的方法。如梯度下降法。

# 线性回归

## 方程y=Ax

## 最小二乘法（平方）Least Squares Method

\sum_(n=1)^N（y-y_i）^2

w\hat=(\pmb{X^T}\pmb{X})^-1\pmb{X^T}y

> 让平方误差最小

集成算法

- bagging：套袋法

- boosting：提升算法：增大错误样本的权重同时减小正确样本的权重。与bagging对比boosting可以同时降低偏差和方差，而bagging只能降低模型的方差。但boosting更加容易过拟合。

- 随机森林：应用bagging和多颗决策树

- 梯度提升树

- adaboost：

> adaboost算法与boost算法不同，它是使用整个训练集来训练弱学习器，其中训练样本在每次迭代的过程中都会重新被赋予一个权重，在上一个弱学习器错误的基础熵进行学习来构建一个更加强大的分类器。

# sklearn学习

## 介绍

-  数据分析和数据挖掘

- 用python进行机器学习

> 数据分析和数据挖掘==机器学习==人工智能

## 分类

- classification

- regression

- clustring

- dimensionality reduction

- model selection

- preprocessing