时间复杂度

二分对象  有序

时间复杂度

Early Stopping

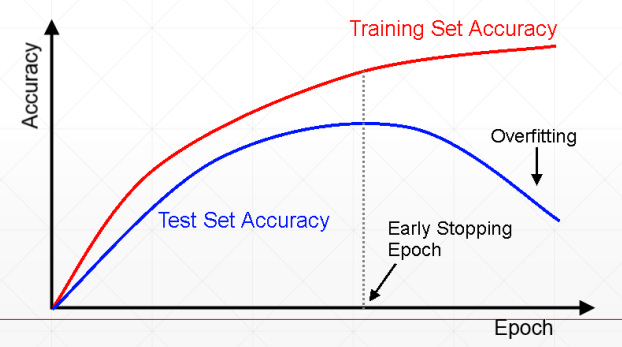
我们要在过拟合之前停止

1、设置val set

2、监听在各个参数值下的val set的表现

3、在val 表现最好的时候停止——一定程度上需要有经验

Dropout——防止过拟合的一种方法

减少了隐藏层之间的神经元的连接量，Learning less to learn more，会使得曲线较为平缓且泛化

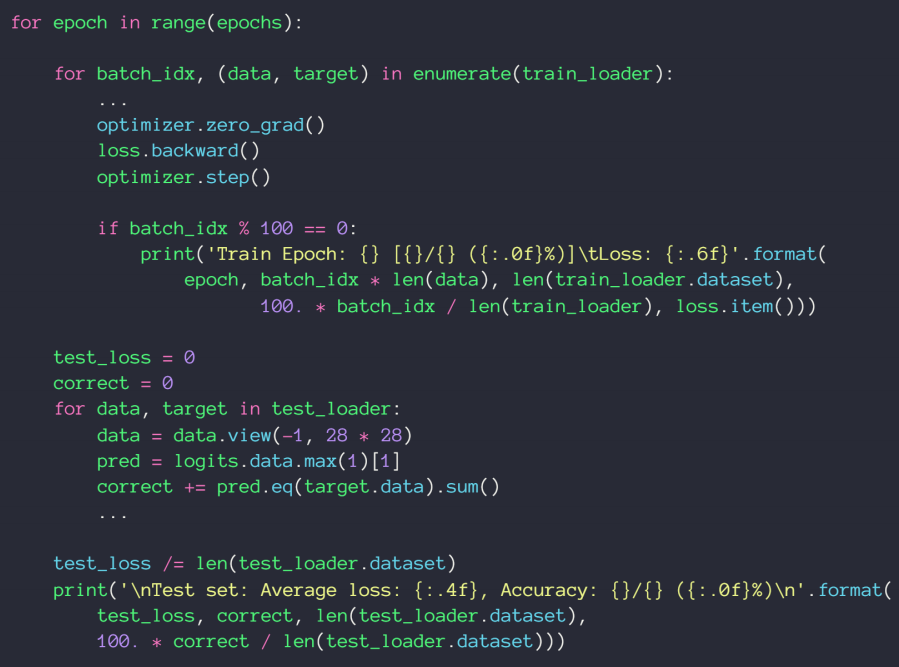
代码实现

需要特别说明的是

在torch里面，p代表的是断掉的概率，在tensorflow里面p代表的是保持连接的概率。

此外，我们约定了在test中，需要全部连接神经，需要手动切断dropout

关键的一句是：net_dropeed.eval( )

Stochastic Gradient Descent并不是完全随机的，而是符合某一个分布的

从train set里面抽取出来一个batch比如16、32、64、128等，计算其所有在某个x上的梯度求和再平均得到梯度值。优点：节约显存

搜索

二分查找/折半查找

有序顺序表

一上来定位中间位置

取得中间元素

7位于序列的中间位置起始是坐标最前面为0

终止位置为8

1 3  4  6 7  8 10 13 14

动量和学习率衰减

动量——惯性

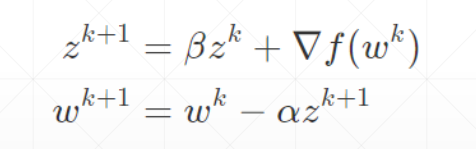
动量是考虑了之前的运动方向的变量

不考虑动量的情况下，会在局部极小值点停止

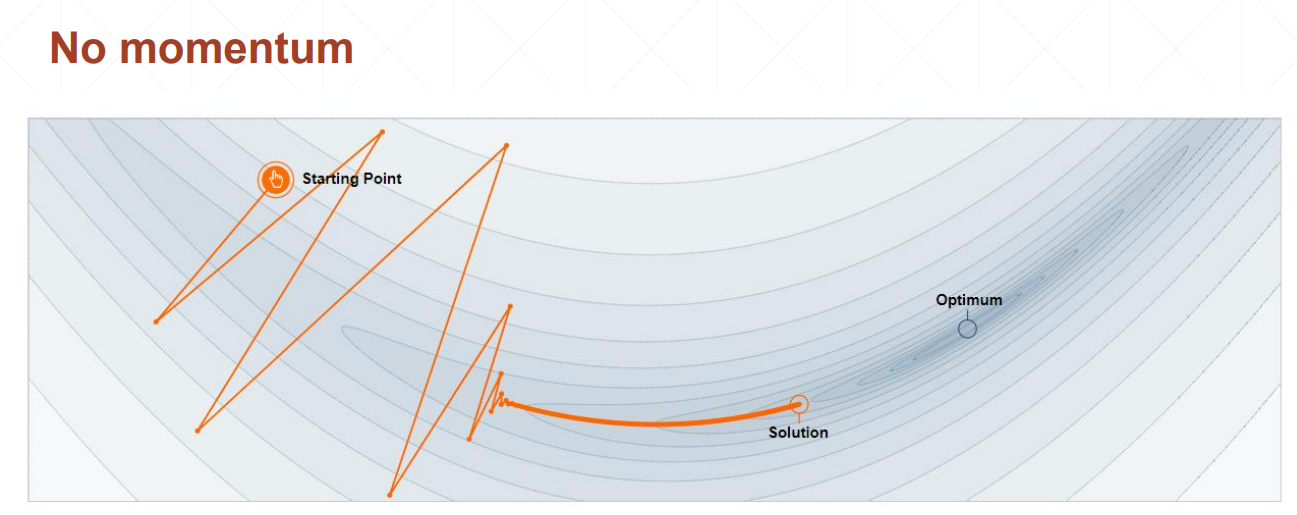
考虑动量的情况下，在局部极小值点处仍然会向前走，比较容易找到全局最优解

优化器中SGD没有考虑动量，可以自己加momentum参数，Adam里面考虑了动量因素，不需要手动加

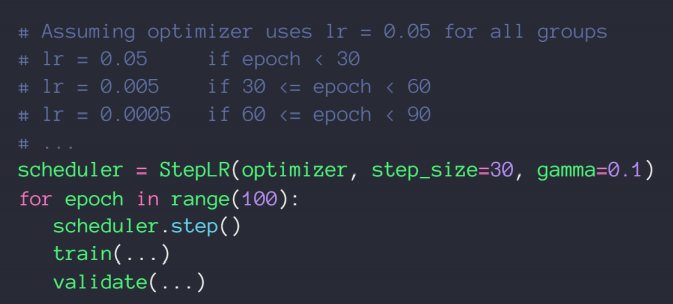
学习率衰减——迫使学习率逐渐变为0

这这里我们并不能指明最合适的学习率，但我们可以让学习率递减，好处是可以较快得找到更好的解

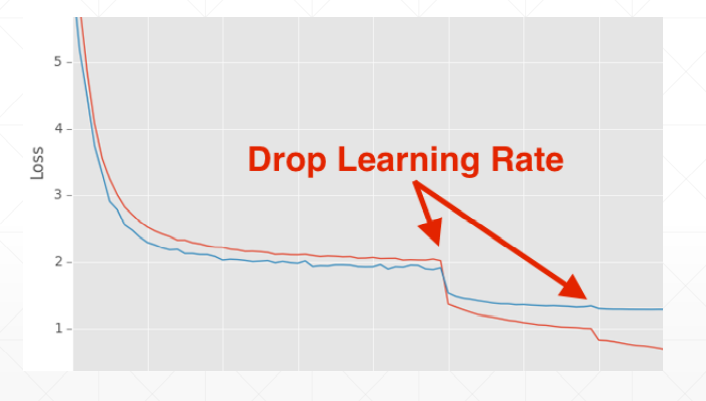
方法一：使用ReducelROnPlateau()函数，传入optimizer 和min，前者用来识别学习率的值，后者用来监听loss，当在某一个学习率上在一定的步长范围内，loss都没有很明显的变化，我们的函数将会自动调整学习率；

方法二：直接规定一个确切步长，确定一个变化率

如何减轻过拟合？Regularization泛化

Occam's Razor：
more thing should not be uesd than are necessary 任何不必要的都不需要

1、提供更多的数据——这是代价做大、也是最困难的方法；

2、简化模型

shallow模型不需要用太复杂的，尤其是当数据集有限的时候。shallow是一个相对的概念，跟数据集大小和网络的复杂度有关。

regularization

我们一开始的目标是最小化交叉熵，下面是目标函数：

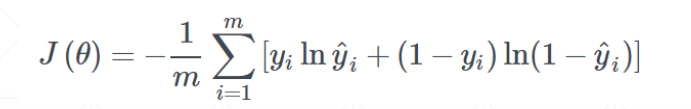
但经过训练之后，为了增强模型的表达能力，很可能出现一个7次方的函数式

接下来我们增加一个参数范式，这里的参数有w1,b1,w2,b2等等

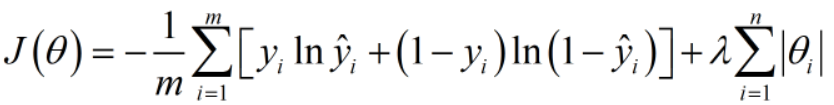
可以是一范数，可以是二范数。

优势1：当我们的总目标是尽可能小化J（Q）时，一范式参数值也会尽可能得小，总体来说会使我们的模型更加平缓和稳定，更加具有总体数据代表性。

优势2：会简化模型，有可能将高次方模型转变为低次方模型，同时还能保持模型的表达性

常用的有一范式和二范式

L2_regularization

这个wieght_decay是二范式的参数值，传入这个参数就可以以二范式进行泛化了

L1_regularization

现阶段没有参数一范数的现成代码，需要自己敲

3、Dropout——增加鲁棒性

4、Data argumentation——数据增强

5、Early Stopping——提前终结

K-flod cross-validation

交叉检验第一次切分的train set 和 val set可以重新整合之后再次随机切分，长时间来说，每个数据都有可能参与到训练中，防止了模型死记硬背，还能充分利用现有的数据集，这样增加了训练的准确性。

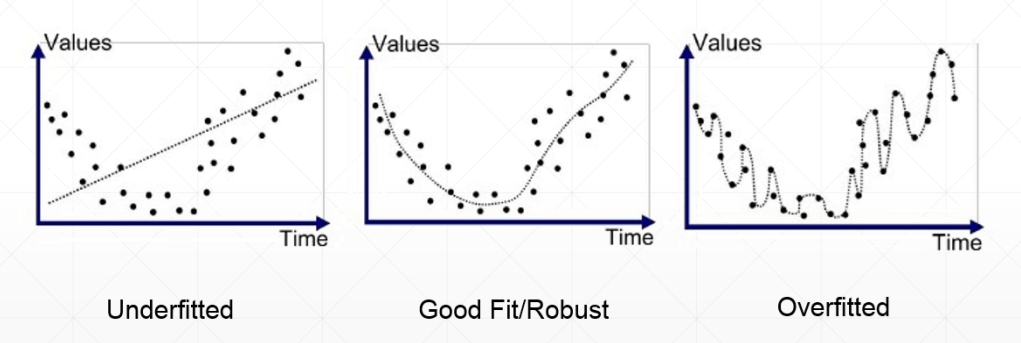
怎样检测过拟合？

通过测试集中的准确率来检测学习情况，提前终止overfitting的情况，我们往往会选取准确率达到最大值的参数为模型的最佳参数值，用来提供给客户做预测检验

上述是我们教学过程中的实验，只有两个数据集，traning和test（这里的test也是val set），但是在实际应用中，我们通常有三个数据集，train set用来学习，val set用来挑选最佳参数和模型，最后由用户的test set来进行检验

最终交付给test set之后是不能反馈准确率的，否则在此基础上再次挑选参数和模型，这个test set的作用和val set就一样了——数据污染，某种程度上讲，是一种作弊

欠拟合：使用模型的复杂度小于真实模型的复杂度

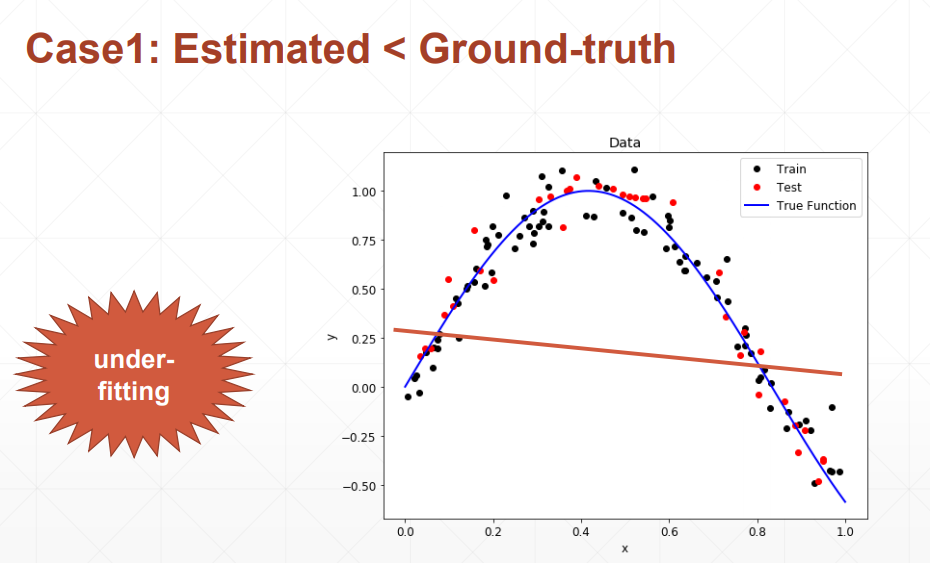
体现在：训练集的loss和准确率都不够理想；测试集的loss和准确率也不理想。

过拟合：使用模型的复杂度大于真实模型的复杂度

体现在：train训练的时候loss和准确率都表现得非常好，但是在测试集上变现得特别不好——泛化能力较差（Generalization Performance）

现实生活中，更多的情况是overfitting。数据集有限，包含了噪声会被模型学习到。

全连接层

nn.Linear(in, out)

简便方法：

Binary Classification

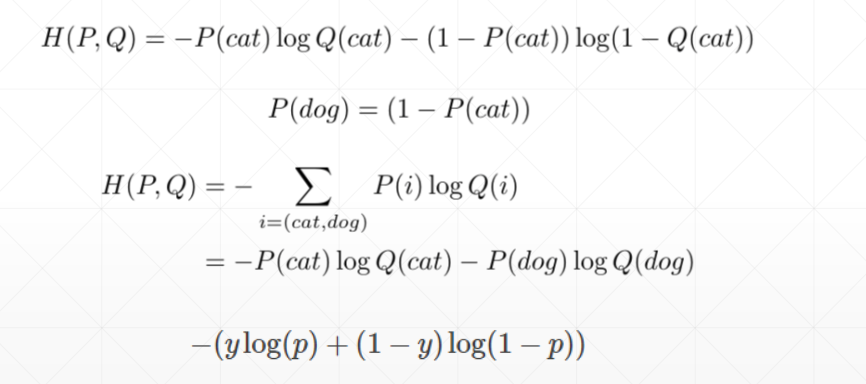
这里的p值是最后的通过激活函数之后的概率值

y是0或1（one—hot编码）

交叉熵从0.916到0.02时，越接近于我们的目标：

是变好的过程

Entropy——熵，指不确定性

熵大则信息量量比较小，越稳定，越没有惊喜度

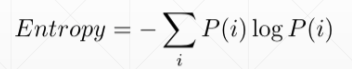
Cross Entropy

Dkl表示的是两个概率分布的距离，当两个概率分布完全相同的时候，距离为0，Dkl=0

当P=Q时：corss Entropy=Entropy

即H（p,q）=H(p)

且在0ne—hot编码规则下H（p）=0， 那我们优化的目标是：

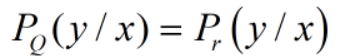
线性回归和逻辑归回/分类问题的区别：

1、函数式不同：

linear regression

y=wx+b；

ligistic regression——在线性回归的基础上加了一个激活函数

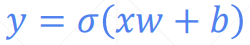
2、目标不同：

线性回顾的目标是预测值接近于真实值；

逻辑回归问题的目标是在x的条件下训练得到y值的概率和当自变量为x时，真实的等于y的概率之间差值最小

无法直接最大化准确率：

准确率的公式为：

分母为所有的y值，分子为预测值等于真实值的个数

（1）存在梯度为0的情况；

计算得到的p=0.4，调整权重之后得到0.45，虽然概率增加了，但是accuray没有发生变化

（2）也有可能存在梯度爆炸的情况

当p值从0.499变动到0.501时，准确的个数增加了一个，当y值（=5）数量较少是，准确个数从3变为4，那么准确率从0.6变动到0.8，准确率变化了0.2，而概率值变动了0.002，则会存在断层连续的情况，也就是梯度爆炸

多类别分类问题——softmax激活函数

2D函数优化实例

反向传播

这里的激活函数统统是sigmoid

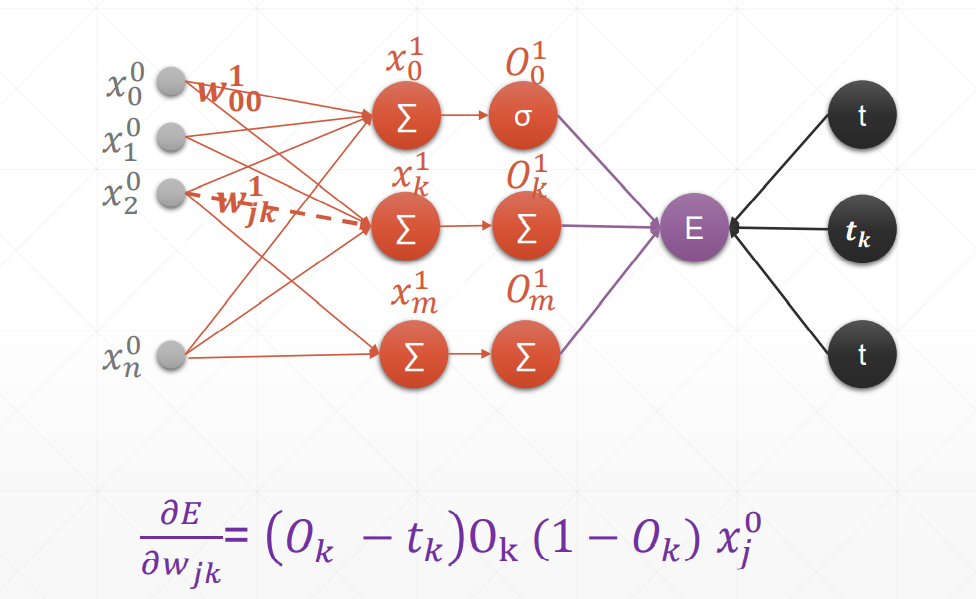
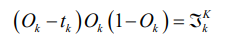
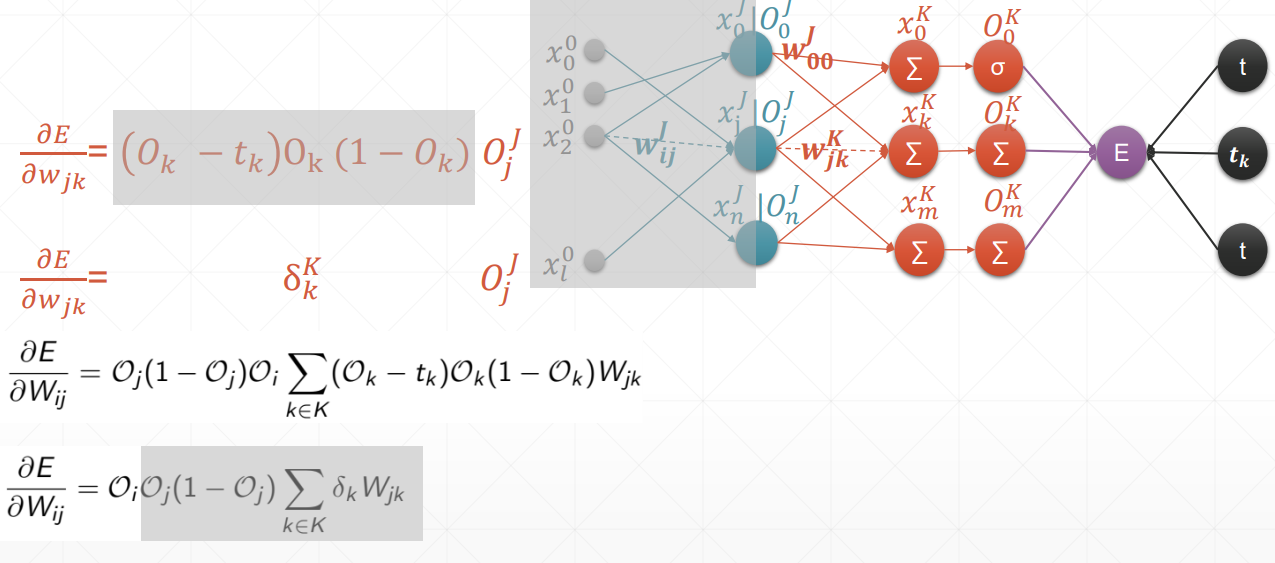
总结：在案例中，oi是输入层，但我们要求得是一个广泛使用的式子，也就是说，在这里我们认为oi是隐藏层。

链式法则

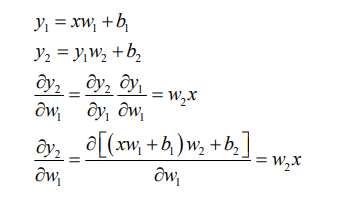
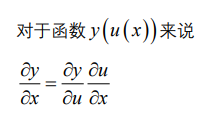
多输出感知机的梯度推导

激活函数仍然是sigmoid，且y的估计函数用到的仍然是一次线性回归函数

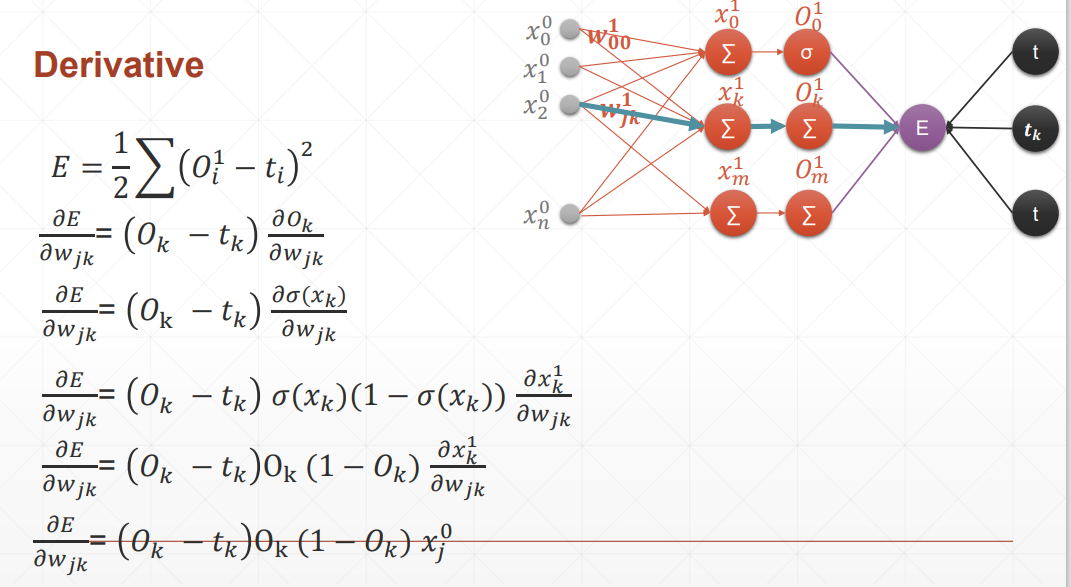
感知机的梯度推导

这里的激活函数是sigmoid激活函数，所以对其求到的结果是，且使用的回归函数是一次线性回归函数。

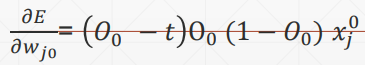
求导

softmax的公式为：

当i=j的时候求导结果为：

当i不等于j的时候求导结果为：

softmax

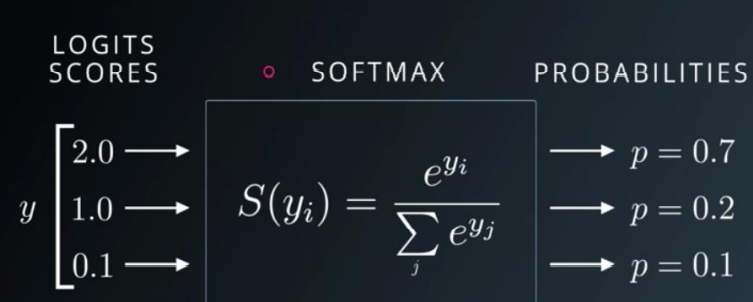
扩大了值之间的差距