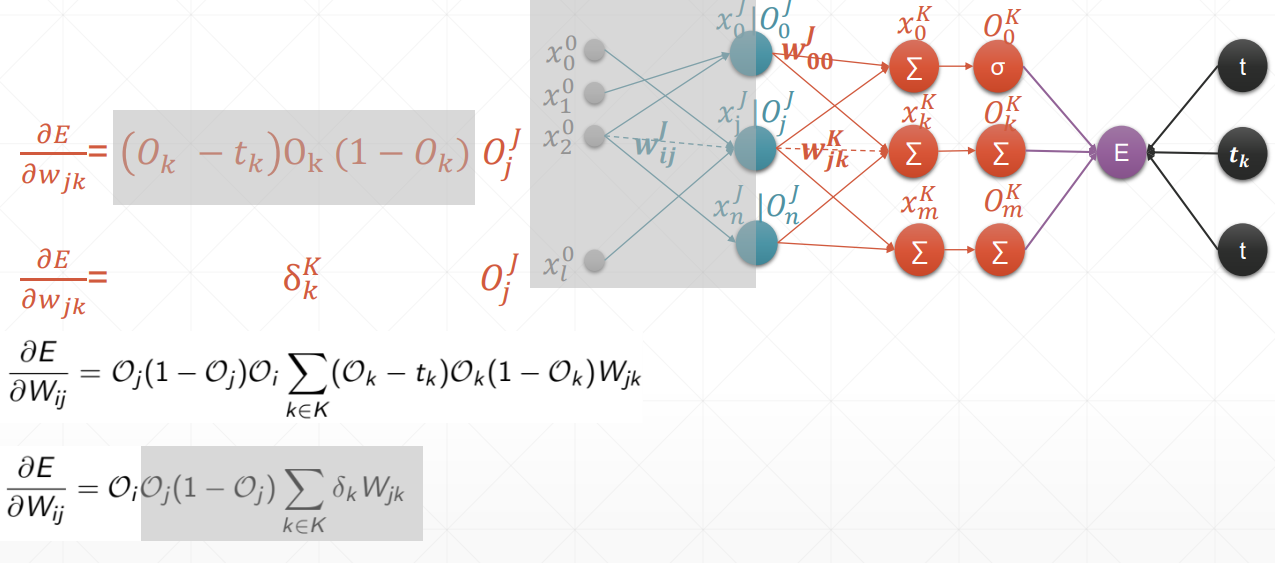
反向传播

这里的激活函数统统是sigmoid

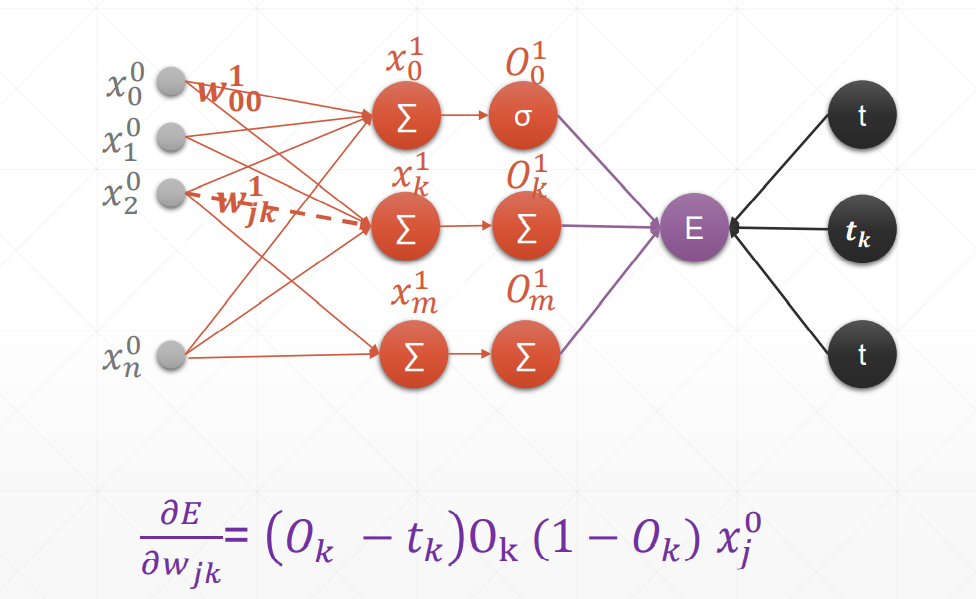
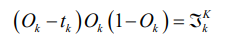
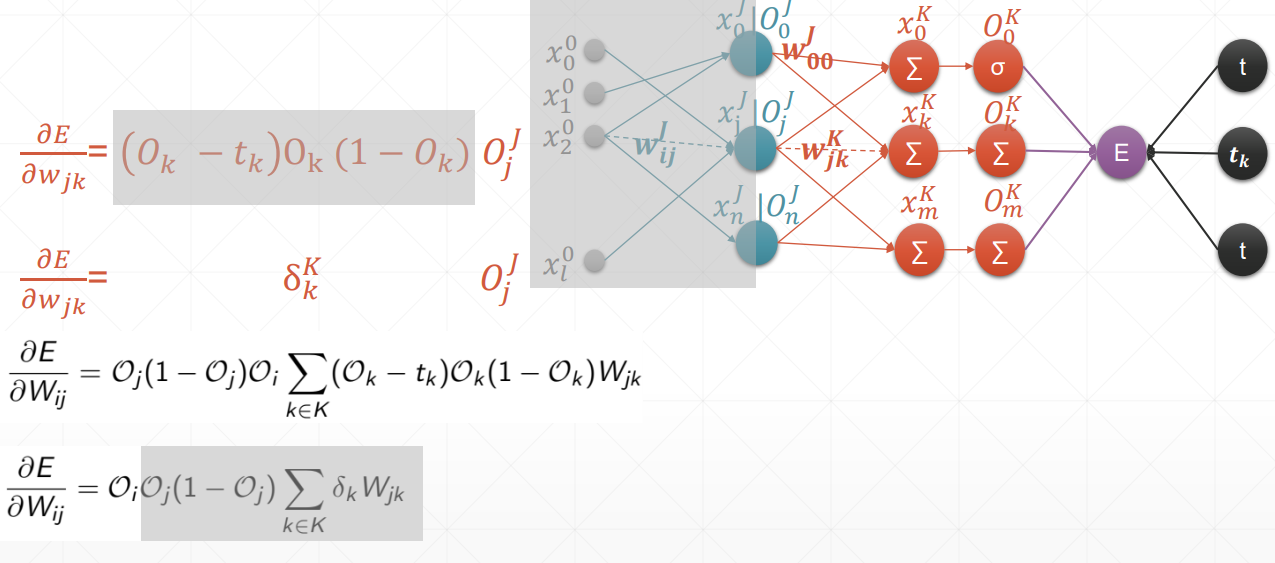
总结：在案例中，oi是输入层，但我们要求得是一个广泛使用的式子，也就是说，在这里我们认为oi是隐藏层。

链式法则

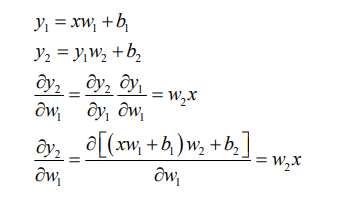
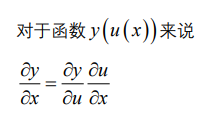
多输出感知机的梯度推导

激活函数仍然是sigmoid，且y的估计函数用到的仍然是一次线性回归函数

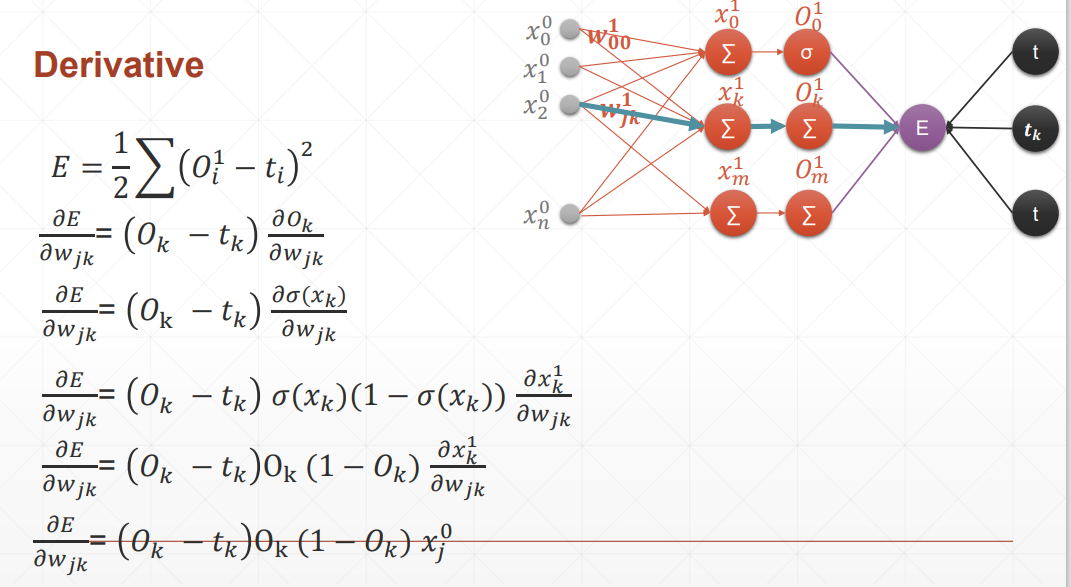
感知机的梯度推导

这里的激活函数是sigmoid激活函数，所以对其求到的结果是，且使用的回归函数是一次线性回归函数。

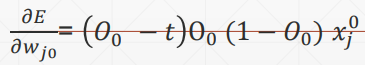
求导

softmax的公式为：

当i=j的时候求导结果为：

当i不等于j的时候求导结果为：

softmax

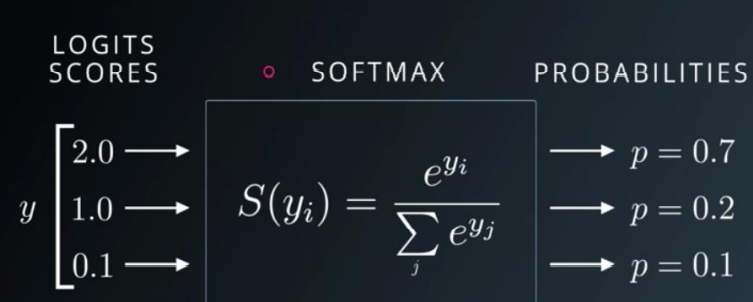
扩大了值之间的差距

loss及其梯度

典型的loss函数 有：

（1）均方差

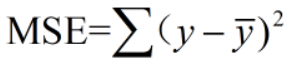
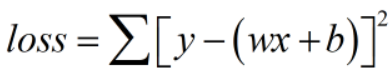
注意：MSE不同于二范数

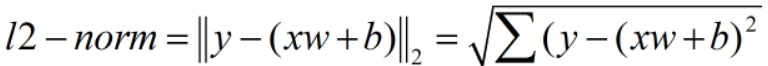
MSE不开根号！

求导

（2）Cross Entropy Loss

可以用于二分类、多分类问题，经常使用softmax激活函数

激活函数及其梯度

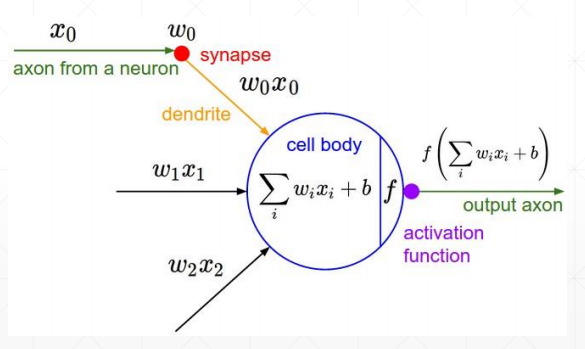
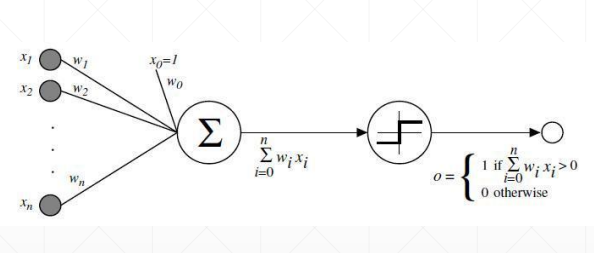
为了解决激活函数不可导的情况，提出了sigmoid/logistic：光滑可导的函数，且把无穷的值域压缩到[0, 1]的范围内

但是会出现梯度离散的情况，参数无法得到更新，因为越往后，导数值与接近于0

sigmoid函数求导之后如下：

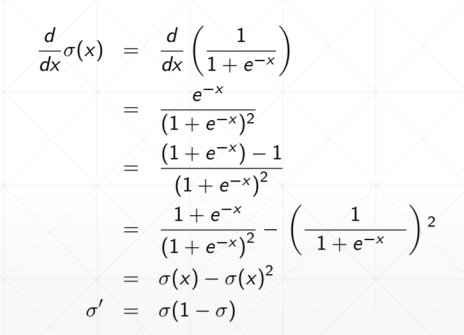
Tanh在RNN里面用得比较多

求导：

Relu使用最多的激活函数

计算导数的时候非常简单，导数为1。不会放大也不会缩小，很大程度上减少了梯度爆炸和梯度离散发生的可能性

常见函数的梯度

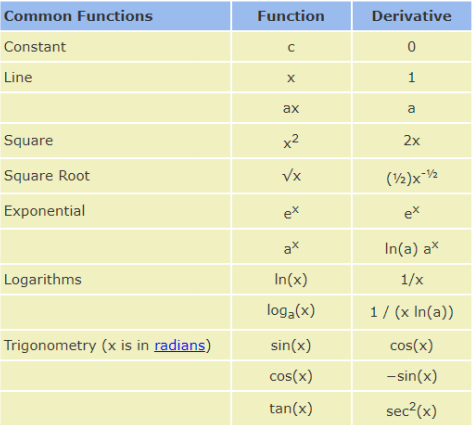
满足上述条件的函数叫做凸函数，不管从哪个方向都能找到全局最优解

容易出现的问题：

（1）有可能会遇到局部最优解

（2）saddle point出现鞍点，在一个自变量上的偏微分取得极大值，在另一个自变量上取极小值

优化梯度下降法来找到全局最优解的因素：

（1）初始状态；

（2）学习率；

（3）momentum——如何逃离局部最小值

什么叫梯度

导数——反映的是随着x的变化，y的变化趋势

偏微分——指定了自变量的方向上，因变量在某个自变量方向上的变化趋势

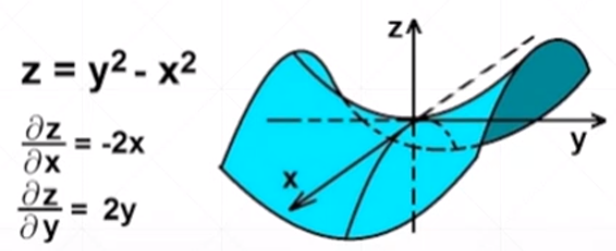
梯度——把所有的偏微分看做向量

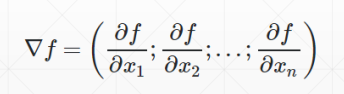
dim、keepdim

当我们指定维度之后返回的最大值和最小值，会自动消减一个维度，如果对一个二维数组取最大值之后，还想保持它的维度是两个，那么我们可以设置keepdim=True

统计属性

常见的统计属性：
norm——范数

注意：norm不等于normalize（正则化）

vector norm 不等同于 matrix norm

（1）第一范数

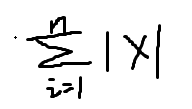
（2）第二范数

mean——均值

sum——求和

max——最大值

min——最小值

argmin——最小值的位置

argmax——最大值的位置

kthvalue——第几个的数值和位置

topk——top几的位置和数值

二维以上的tensor matul

matmu完成二维以上的矩阵相乘运算，但事实上，我们实际运算的也是最后两个维度的数值

近似值

floor（）取小

ceil（）取大

round（）四舍五入

trunc（）取整数

frac（）取小数

裁剪——clamp

打印参数w的梯度：w.grad.norm(2)

torch里面的clamp类似于numpy里面的climp把数值范围进行裁剪 

数学运算

（1）加减乘除

（2）矩阵相乘 matmul 是按照矩阵的方式相乘

·Torch.mm（只适用于二维矩阵，不建议使用）

·Torch.matmul

·@

一个案例

stack和cat的区别

cat在指定维度上可以值不同，但是stack在指定维度上的值必须相同

拼接和拆分

cat

从最小维度开始匹配，我们默认越高维度越相似，而小维度上各有各的不同

[32, 32]给每行每列加一个base基底；

[3, 1, 1]相等于是给每个通道都加个值；

[1, 1, 1, 1]像素点增加了一个值

why broadcasting

（1）本身有现实意义；

（2）可以节省内存消耗

什么情况下需要将broadcasting？

match from last dim!

·如果当前的dim=1，扩展相同的维度

·如果其他地方没有维度，可以添加这一个模块，然后扩展成相同维度

·否则，则不能进行传播