洛贝达法则
泰勒展开
洛贝达法则
泰勒展开
费马定理
当x取极值时,f(x)的导数等于0
https://www.derivative-calculator.bet/
求导
import sympy as sp
数据增强
神经网络对数据的要求非常饥渴,需要贴有标签的大量数据
当数据量有限的时候:1、要减少神经网络的隐藏层;2、Regularization,迫使一部分权值接近于0,让网络的表现更加稳定;3、数据增强,目前的数据量较少,想办法对数据进行变换——旋转、裁剪加噪声等
Flip——翻转
可以从水平方向和竖直方向进行翻转,这里增加了random属性,代表翻转是具有随机性的,有可能进行水平翻转,也有可能不翻转,有可能垂直翻转,也有可能不翻转
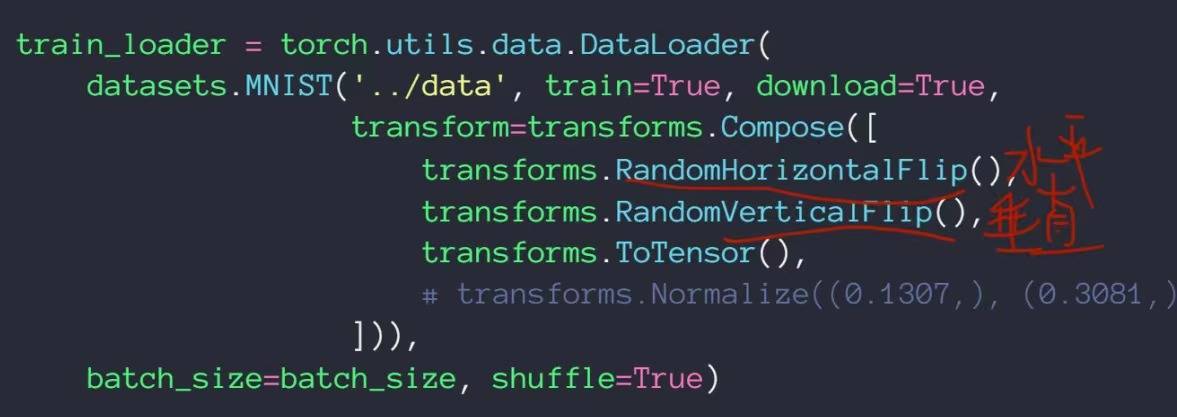
Rotate——旋转
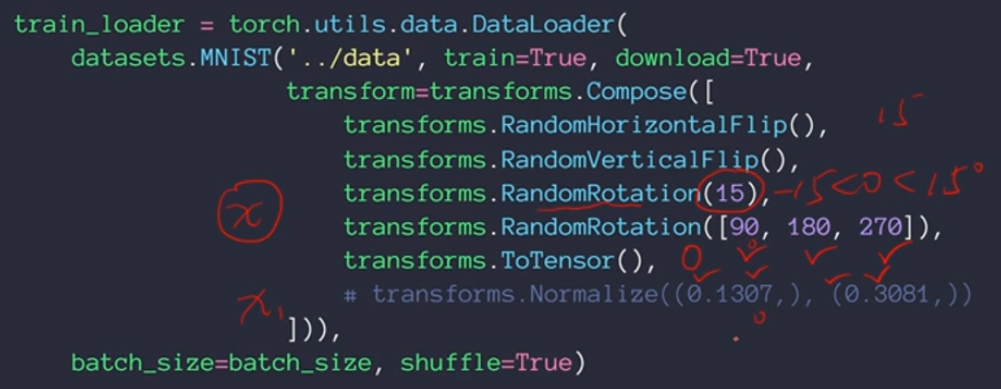
Scale——缩放
以中心点为标准进行缩放Resize,传入的是list

Crop Part
随机得进行裁剪
transform是torchvision里面自带的包, transform.Compose()可以把一系列翻转、旋转、裁剪和缩放操作组合在一起

Noise——加噪声,用的不多
即使得到了无穷多的数据,由于进行变换后的数据和原本的数据非常接近,所以训练的结果仅仅能得到一个很小的提升
4、save和load

5、train和test状态切换很方便

6、implement own layer
由于实际需要定义一个flatten类,我们通过nn.Sequential()来把函数有序排列起来组成我们主要的神经网络结构
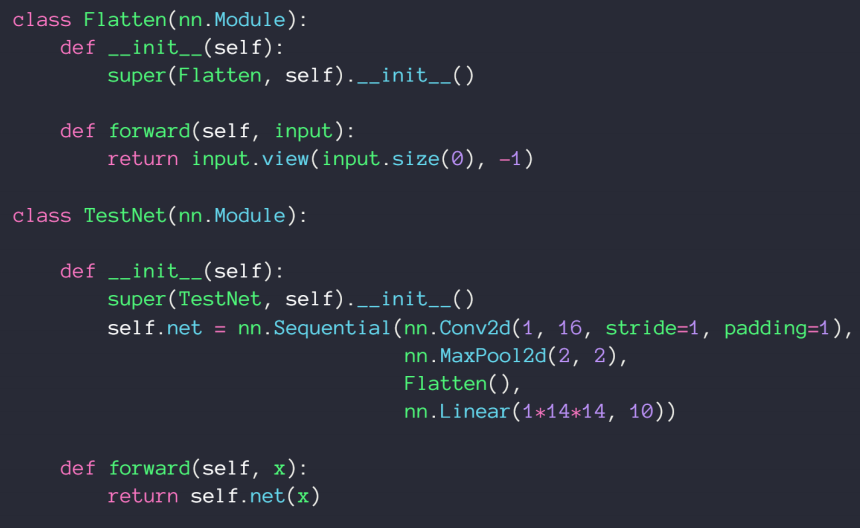
7、通过nn.Parameter( )实现自己的参数定义

nn.Module的好处
提供了很多现成的网络层

1、container——nn.Sequential()
将神经网络内部的结构按照顺序进行编码
net = nn.Sequential()可以直接实现网络前向传播
2、其次,通过net.parameters( )可以返回想要的参数;也可以通过net.parameters( )把参数丢到优化器里
3、modules里面包括了所有的节点;里面包括很多子节点——直系亲属

整个net有5个节点

DenseNet跟ResNet一样都有shortcut短接,以使得及时是很深的网络其性能也不必浅层的网络差,不一样的是后面的每一层网络都有可能与前面任意一层网络形成短接

最上面的没有短接的神经网络
第二个是Resnet
最后一个是DenseNet
从图片上可以看出来区别
VGG
研究发现卷积核较小的时候不仅可以提高运算量,且对图片benshen

GoogLeNet
在每个隐藏层都使用了不同大小的卷积核,从不同的视觉大小更深刻得学习图片

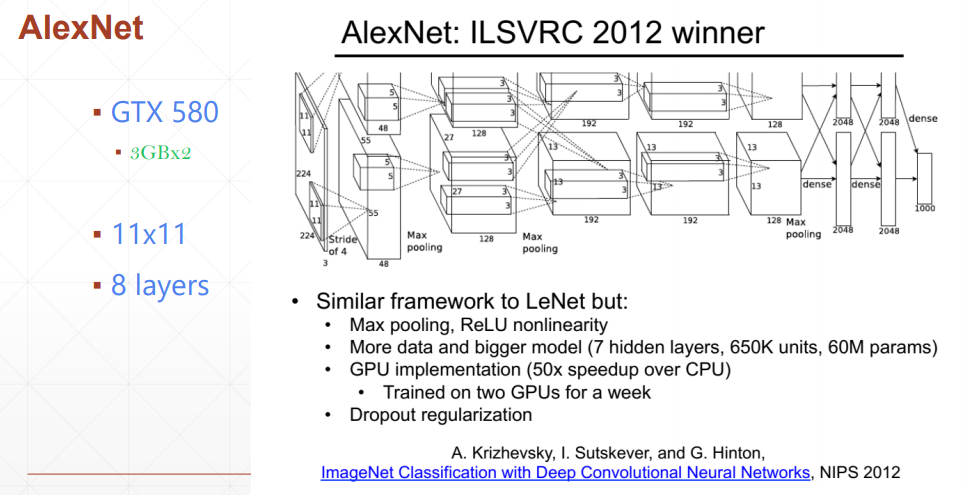
leNet-5将准确率提升了10%+
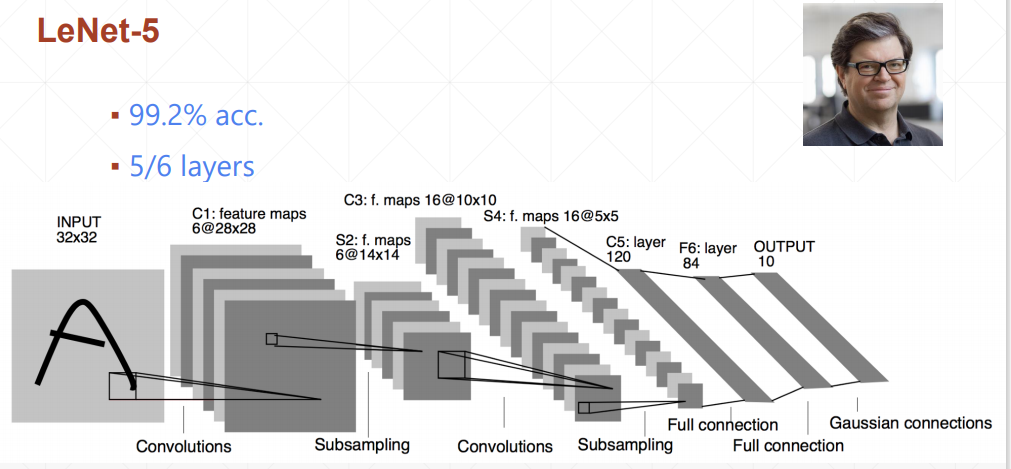
AlexNet使用了下采样层和relu激活函数
Batch Norm有以下四种,只是以哪个维度为标准的区别
 我们主要学习Batch normalization以通道为基准,计算每个通道上的均值和方差,然后通过减均值除以方法来使这些值均匀得分布在某个范围内
我们主要学习Batch normalization以通道为基准,计算每个通道上的均值和方差,然后通过减均值除以方法来使这些值均匀得分布在某个范围内
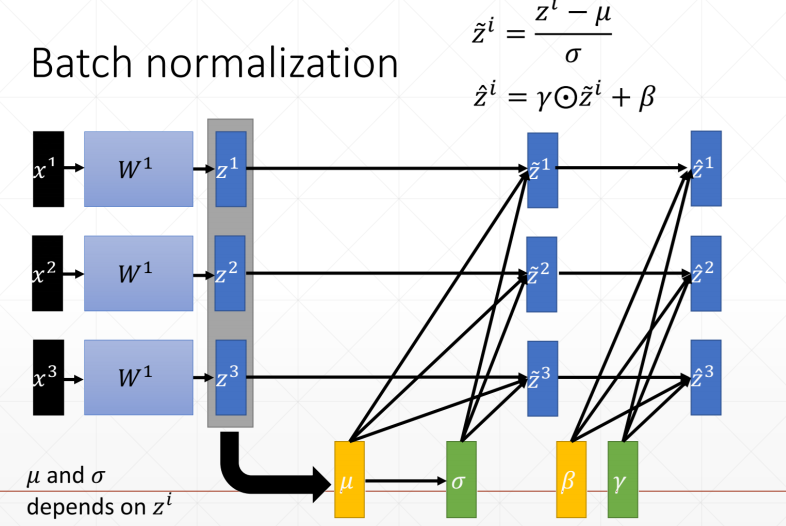
规范化算法 计算均值和方差、标准化、 缩放

在测试集上,我们把训练集的runnnig_mean/running_var直接赋值给训练集,test没有backward,所有w和b并不需要更新,不需要梯度更新
BatchNorm
将不同维度的值都缩放到一个以0为均值,以某个值为方差的比较均匀的分布上
Feature scaling
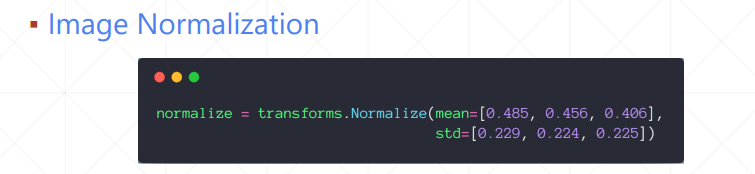
输入R、G、B各通道的均值和方差,normaliazation的具体过程是
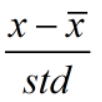
池化层(pooling)
向下采样:
Max pooling
采集的是窗口内的最大值
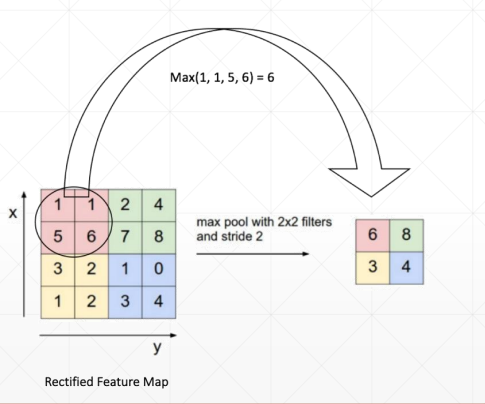
Avg pooling
采集的是窗口数值的均值
向上取样,把图片方法,取最近距离的值进行简单的复制
Multi-Kernels
每一个通道上都需要有相同的卷积核,每个通道可以有1个2个甚至更多的卷积核,但是每个通道上的卷积核都必须相同!每个核之间可以不同

概念:
Input_channels输入的通道(黑白图有1个通道,彩图RGB有三个通道)
Kernel_channels有多少个核(边缘核、模糊核都有就是两个核)
Kernel_size核的大小,2x2,或者是3x3
stride:步长
Padding(打补丁):在两边补空白的数量,2列是2,1行是1
卷积原理:
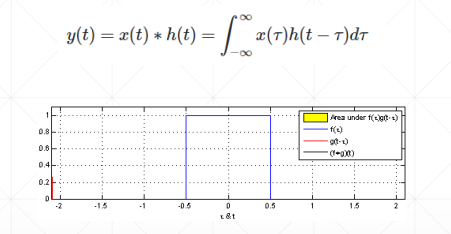
神经网络里的卷积是离散数值,是小窗口的矩阵相乘相加操作
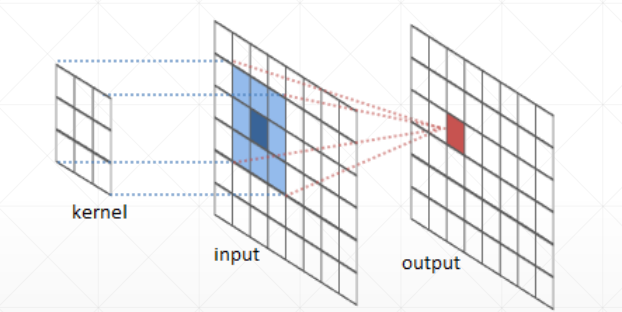
卷积神经网络中f(x,y)里面的x和y分别是距离坐标原点的距离(偏置)
Early Stopping
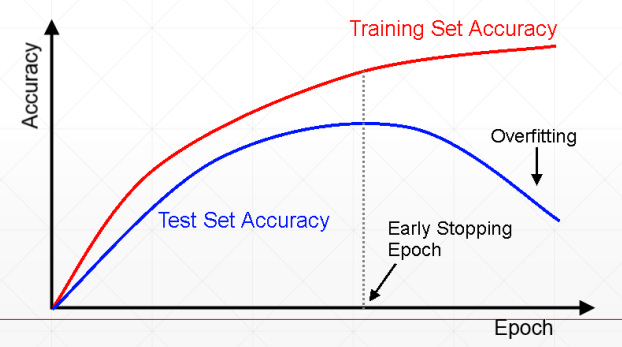
我们要在过拟合之前停止
1、设置val set
2、监听在各个参数值下的val set的表现
3、在val 表现最好的时候停止——一定程度上需要有经验

Dropout——防止过拟合的一种方法
减少了隐藏层之间的神经元的连接量,Learning less to learn more,会使得曲线较为平缓且泛化

代码实现

需要特别说明的是
在torch里面,p代表的是断掉的概率,在tensorflow里面p代表的是保持连接的概率。

此外,我们约定了在test中,需要全部连接神经,需要手动切断dropout
关键的一句是:net_dropeed.eval( )

Stochastic Gradient Descent并不是完全随机的,而是符合某一个分布的
从train set里面抽取出来一个batch比如16、32、64、128等,计算其所有在某个x上的梯度求和再平均得到梯度值。优点:节约显存

动量和学习率衰减
动量——惯性
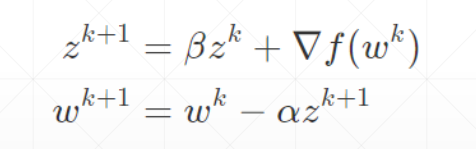
动量是考虑了之前的运动方向的变量
不考虑动量的情况下,会在局部极小值点停止
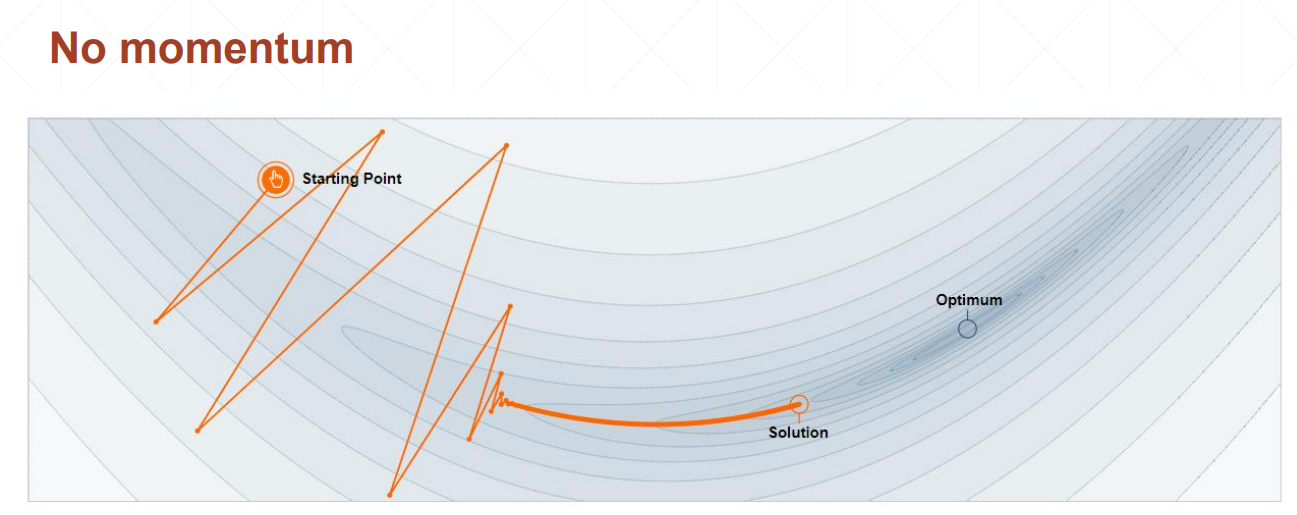
考虑动量的情况下,在局部极小值点处仍然会向前走,比较容易找到全局最优解

优化器中SGD没有考虑动量,可以自己加momentum参数,Adam里面考虑了动量因素,不需要手动加

学习率衰减——迫使学习率逐渐变为0

这这里我们并不能指明最合适的学习率,但我们可以让学习率递减,好处是可以较快得找到更好的解
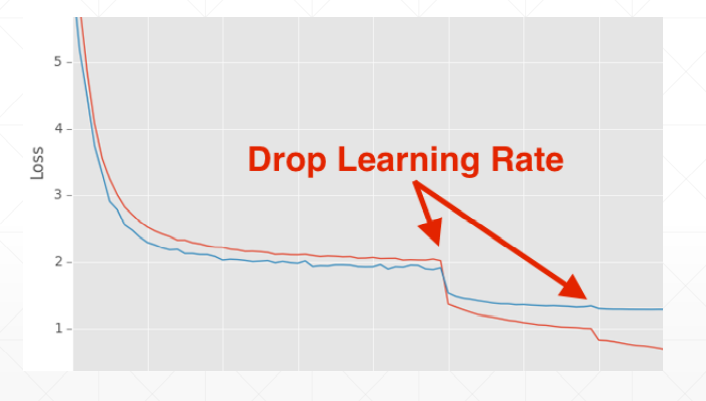
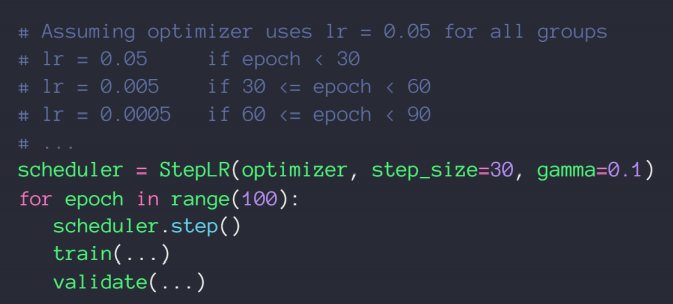
方法一:使用ReducelROnPlateau()函数,传入optimizer 和min,前者用来识别学习率的值,后者用来监听loss,当在某一个学习率上在一定的步长范围内,loss都没有很明显的变化,我们的函数将会自动调整学习率;

方法二:直接规定一个确切步长,确定一个变化率
如何减轻过拟合?Regularization泛化
Occam's Razor:
more thing should not be uesd than are necessary 任何不必要的都不需要
1、提供更多的数据——这是代价做大、也是最困难的方法;
2、简化模型
shallow模型不需要用太复杂的,尤其是当数据集有限的时候。shallow是一个相对的概念,跟数据集大小和网络的复杂度有关。
regularization
我们一开始的目标是最小化交叉熵,下面是目标函数:
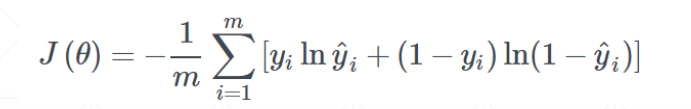
但经过训练之后,为了增强模型的表达能力,很可能出现一个7次方的函数式
接下来我们增加一个参数范式,这里的参数有w1,b1,w2,b2等等
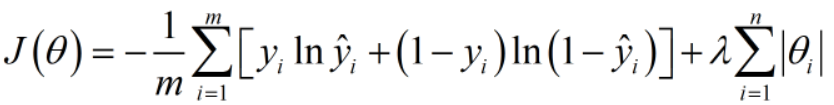
可以是一范数,可以是二范数。
优势1:当我们的总目标是尽可能小化J(Q)时,一范式参数值也会尽可能得小,总体来说会使我们的模型更加平缓和稳定,更加具有总体数据代表性。
优势2:会简化模型,有可能将高次方模型转变为低次方模型,同时还能保持模型的表达性
常用的有一范式和二范式

L2_regularization
这个wieght_decay是二范式的参数值,传入这个参数就可以以二范式进行泛化了
L1_regularization
现阶段没有参数一范数的现成代码,需要自己敲

3、Dropout——增加鲁棒性
4、Data argumentation——数据增强
5、Early Stopping——提前终结
K-flod cross-validation
交叉检验第一次切分的train set 和 val set可以重新整合之后再次随机切分,长时间来说,每个数据都有可能参与到训练中,防止了模型死记硬背,还能充分利用现有的数据集,这样增加了训练的准确性。