【10,20,30,40,50,60,70】【-5:-3】
##倒数第五和倒数第三,包头不包尾
结果:【30,40】
【10,20,30,40,50,60,70】【::-1】
##反向提取
结果:【70,60,50,40,30,20,10】
#print列表的遍历
【10,20,30,40,50,60,70】【-5:-3】
##倒数第五和倒数第三,包头不包尾
结果:【30,40】
【10,20,30,40,50,60,70】【::-1】
##反向提取
结果:【70,60,50,40,30,20,10】
#print列表的遍历
#account 计数 #len 列表长度
##index()获得指定元素在列表中首次出现的索引
a = ["明天出去吗?","不,要去做核酸"]
a.remove('明天出去吗?')
a
#bin(c)#打印二进制数
bin(c&b)
bin(c^b)亦或,相同是0,不相同是1
左移相当于*2右移相当于/2
a==3
a<<3
#字符串拼接
“3”+“2”==“32”
【10,20,30】+【5,10,100】=【10 20 30 5 10 100】
#乘法
“sxt”*3 =sxtsxtsxt
【10,20,30】*2=【10,20,30,10,20,30】
io.StringIO 可变符号串
例如:
s = 'hello.sxt'
import io
sio = io.StringIO(s)
sio
a='abcdfehunlnklnaskdkl'
a[1:5]
a[-5:]
del 变量名 #删除
算法的五大特性:输入、输出、有穷性、确定性、可行性
1.安装与开发环境
阿斯蒂芬
支持向量机的分类方法,是在这组分布中找出一个超平面作为决策边界,使模型在数据上的 分类误差尽量接近于小,尤其是在未知数据集上的分类误差(泛化误差)尽量小。

决策边界一侧的所有点在分类为属于一个类,而另一侧的所有点分类属于另一个类。如果我们能够找出决策边界, 分类问题就可以变成探讨每个样本对于决策边界而言的相对位置。比如上面的数据分布,我们很容易就可以在方块 和圆的中间画出一条线,并让所有落在直线左边的样本被分类为方块,在直线右边的样本被分类为圆。如果把数据 当作我们的训练集,只要直线的一边只有一种类型的数据,就没有分类错误,我们的训练误差就会为0。
但是,对于一个数据集来说,让训练误差为0的决策边界可以有无数条。
支持向量机(SVM,也称为支持向量网络),是机器学习中获得关注最多的算法没有之一。它源于统计学习理论, 是我们除了集成算法之外,接触的第一个强学习器。它有多强呢?

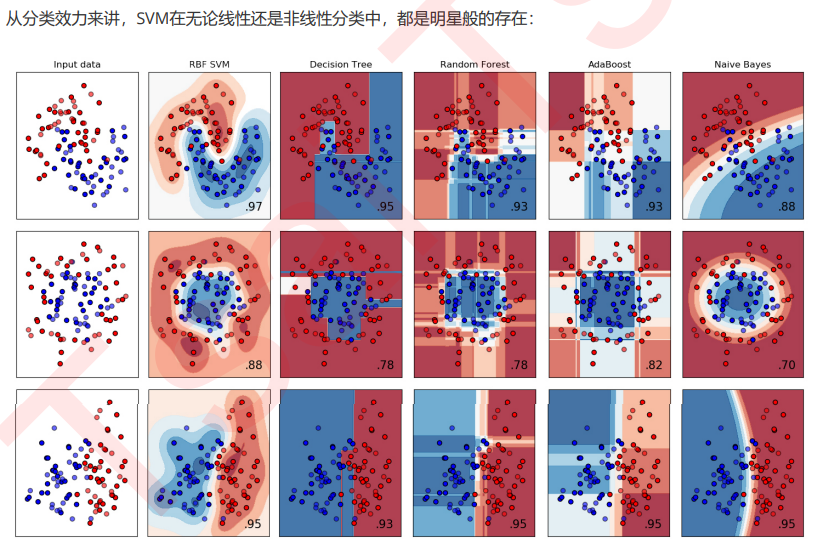
从实际应用来看,SVM在各种实际问题中都表现非常优秀。它在手写识别数字和人脸识别中应用广泛,在文本和超 文本的分类中举足轻重,因为SVM可以大量减少标准归纳(standard inductive)和转换设置(transductive settings)中对标记训练实例的需求。同时,SVM也被用来执行图像的分类,并用于图像分割系统。。除此之外,生物学和许多其他科学都是SVM的青睐者,SVM现在已经广泛被用于蛋白质分类,现 在化合物分类的业界平均水平可以达到90%以上的准确率。在生物科学的尖端研究中,人们还使用支持向量机来识 别用于模型预测的各种特征,以找出各种基因表现结果的影响因素。
从学术的角度来看,SVM是最接近深度学习的机器学习算法。线性SVM可以看成是神经网络的单个神经元(虽然损 失函数与神经网络不同),非线性的SVM则与两层的神经网络相当,非线性的SVM中如果添加多个核函数,则可以 模仿多层的神经网络。
类方法:从属于“类对象”的方法,格式如下:
@classmethod
def 类对象(cls,[,形参列表]):
函数体
要点如下:
(1)@classmathod必须位于方法上面一行
(2)第一个cls必须有;cls指的就是“类对象”本身;
(3)调用类方法格式:“类名.类方法名(参数列表)”,不需要给cls传值。
类对象
实例方法(从属于实例对象)
def 方法名(self,[形参列表]):
函数体
实例属性:从属于实例对象,也成为实例变量。
(1)实例属性一般在__init__()方法中通过如下代码定义:
self.实例属性名=初始值
(2)在本类的其他实例方法中,也是通过self进行访问:
self.实例属性名
(3)创建实例对象后,通过实例对象进行访问:
obj01=类名() #创建对象,调用__init__()初始化属性
obj01.实例属性名=值 #可以给已有属性赋值,也可以新加属性
构造函数__init__():初始化实例对象的实例属性。
Python对象包含三个部分=id、type、value
只要是类中的方法参数第一个都是self,通过类名()来调用构造函数
对象的进化
面向对象
Python支持面向过程、面向对象、函数式编程等多种编程范式。