二维以上的tensor matul
matmu完成二维以上的矩阵相乘运算,但事实上,我们实际运算的也是最后两个维度的数值
近似值
floor()取小
ceil()取大
round()四舍五入
trunc()取整数
frac()取小数
裁剪——clamp
打印参数w的梯度:w.grad.norm(2)
torch里面的clamp类似于numpy里面的climp把数值范围进行裁剪
二维以上的tensor matul
matmu完成二维以上的矩阵相乘运算,但事实上,我们实际运算的也是最后两个维度的数值
近似值
floor()取小
ceil()取大
round()四舍五入
trunc()取整数
frac()取小数
裁剪——clamp
打印参数w的梯度:w.grad.norm(2)
torch里面的clamp类似于numpy里面的climp把数值范围进行裁剪
数学运算
(1)加减乘除
(2)矩阵相乘 matmul 是按照矩阵的方式相乘
·Torch.mm(只适用于二维矩阵,不建议使用)
·Torch.matmul
·@
一个案例
stack和cat的区别
cat在指定维度上可以值不同,但是stack在指定维度上的值必须相同
拼接和拆分
cat
从最小维度开始匹配,我们默认越高维度越相似,而小维度上各有各的不同

[32, 32]给每行每列加一个base基底;
[3, 1, 1]相等于是给每个通道都加个值;
[1, 1, 1, 1]像素点增加了一个值
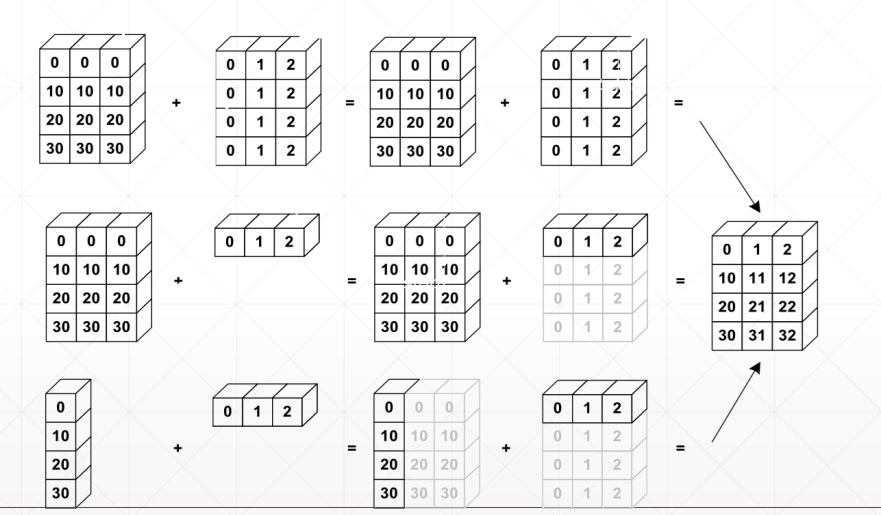
why broadcasting
(1)本身有现实意义;
(2)可以节省内存消耗
什么情况下需要将broadcasting?
match from last dim!
·如果当前的dim=1,扩展相同的维度
·如果其他地方没有维度,可以添加这一个模块,然后扩展成相同维度
·否则,则不能进行传播
broadingcasting
(1)expand
(2)without copying data
key idea

事件:样本点的合集
事件运算:
包含,等价,对立(逆事件)
AUB, A,B事件的并
A∩B=AB,A,B事件的交集
AB=空集, A∪B=A+B 称为和
A-B=AB(逆)
交换律A∪B=B∪A, AB=BA
结合律(A∪B)∪C=A∪(B∪C),ABC=A(BC)
分配律(A∪B)∩C=AC ∩ BC
(A∩B)∪C=(A∪C)∩(B∪C)
德摩根定理:分开反号
同一运算符
is
is not
== 调用 __eq__()方法
整数缓存问题
布尔值
比较运算符
==
!=
>
<
逻辑运算符
or
and
not
短路现象
同一运算符
计算距离:
import math
distance=math.sqrt((x1-x4)**2+(y1-y4)**2)
turtle.write(distance)
时间表示
1970 unix时间点(起始点)
import time
time.time()
秒.微秒
float()
科学计数法
round(3.54)=4四舍五入
增强型赋值运算符
0b二进制
0o八进制
0x十六进制
int()
python3可以储存任意大小的整数
repeat接口
repeat传参的参数是拷贝的次数
转置操作
with open('aa.gif','rb') as f:
with open('aa_copy.gif','rb') as w:
for line in f.readlines():
w.write(line)
print('图片拷贝成功!')
Expand/repeat
Expand——broadcasting仅仅是把数据进行了传播,节约内存
仅仅局限于从1开始扩展,如果是从3拓展的话,是不可行的,会报错
Repeat——实实在在的数据拷贝
squeeze、unsqueeze
for example
数据的存储、维度顺序非常重要,需要时刻谨记
数据类型:
整型、浮点型、布尔型、字符串型
对数字的运算:
+
-
*
/浮点数除法
//整数除法
%模(取余)
**幂
divmod(13,3)同时得到商和余数
(4,1)