https://cloud.189.cn/t/EBF

电信日志分析：

描述：

1. 以什么为基础计算：电信用户上网所产生的数据
2. 数据主要来源：访问日志和安全日志
3. 目的：异常IP的检测、关键词的过滤、违规违法用户的处理
4. 方法：通过Hadoop大数据平台完成日志的入库、处理、查询、实时分析、上报等功能实现
5. 数据量：1T-20T左右
6. 集群数量：10台-100台

项目架构分析：

1. 数据采集层（千兆网卡以上）：
   • 用户访问日志数据：数据格式；
     数据采集的方式：ftp
     数据上传时间
     小文件合并：shell(JNotify)
   • 用户安全日志数据：
     触发上传要求
     数据采集方式：socket--C++完成数据采集，缓存到内存磁盘
     数据格式：加密码加密形式
2. 数据储存层：HDFS分布式文件系统
3. 数据分析层：
   1. MapReduce：数据清洗
   2. HIVE
   3. hbase：固定条件查询
   4. impala：实时性较高的要求
   5. SPARK:解决单一数据源多指标在内存中的计算
   6. OOZIE：任务调度
   7. mysol：HIVE和oozie元数据存放
4. 机器学习层：在大数据的存储和计算基础上，通过构建机器学习构建机器学习模型，对事实作出预判

项目优化：HDFS+SPARK一站式分析平台

机器学习模型=数据+算法

统计学习=模型+策略+算法

模型：规律 y=ax+b

损失函数=误差函数=目标函数

算法：如何高效找到最优参数

决策函数 或 条件概率分布

半监督学习：一部分有类别标签，一部分没有类别标签

主动学习：依赖于人工打标签

聚类的假设：将有标记的样本和无标记的样本混合在一起，通过特征间的相似性，将样本分成若干个组或若干个簇；使得组内的相似性较大，组间的相异性较大，将样本点都进行分组，；此时分组点的样本点即包含了有类别标签的也包含了没有类别标签的，根据有类别标签的样本，按照少数服从多数的原则对没有加标记的样本添加标记。至此，所有未标记的数据都可以加以分配标记。

半监督学习转化为监督学习。

强化学习：解决连续决策问题。

为其可以是一个强化学习问题，需要学习在各种局势下如何走出最好的招法

迁移学习：小数据集：两个相关领域（解决数据适应性问题）

个性化

深度+强化+迁移

监督学习：分类问题、回归

分类：决策树、KNN、贝叶斯、SVM、LR

回归：线性回归、多元回归LASSO回归、RIDGE回归、Elastic回归

无监督学习（非监督学习）：

1、聚类（Kmeans)在没有类别标签的情况下，根据特征相似性或相异性进行分类；

2、特征降维（PCA. LDA)：根据算法将高维特征降低到了低维

机器学习个概念的理解：

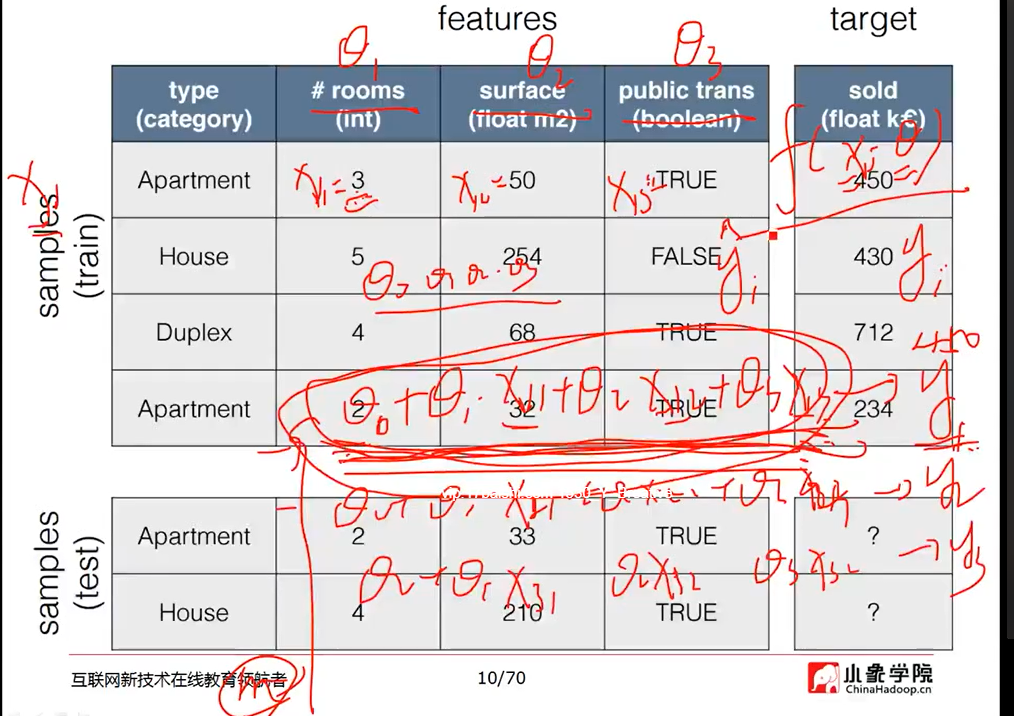
数据集：

定义数据集的名称

行：样本或实例

列：特征或属性，最后一列（类别标签列，结果列）

特征、属性空间：有特征维数所张成的空间

>>特征向量：组成特征火属性空间中的样本点

>>特征值或属性值：组成特征向量中的值

基于规则的学习：它是一种硬编码方式

X 自变量   定义域 特征

Y因变量    值域  结果

fx----f(对应关系)----->y（函数、映射、模型）

基于模型的学习：y=kx+b 寻求k和b的最佳值

通过数据构建机器学习模型，通过模型进行预测；

机器学习学的是模型中的k和

GPU图形图像处理器（处理速度是CPU的10倍以上）

机器学习==CPU+GPU+数据+算法

机器学习：致力于研究如何通过计算（CPU和GPU计算）的手段，利用经验来改善（计算机）系统自身的性能

是人工智能的核心

从数据中产生或发现规律

数据+机器学习算法=机器学习模型

有了学习算法我们就可以把经验数据提供给他，他就能基于这些数据产生模型

如何判断问题是否为机器学习问题？

预测性的

数据：观测值、感知值，测量值

信息：可信的数据

数据分析：对数据到信息的整理、筛选和加工的过程。

数据挖掘：对信息进行价值化的分析

用机器学习的方法进行数据挖掘。机器学习是一种方法，数据挖掘是一件事情；

人工智能包括机器学习，机器学习包括深度学习

机器学习是人工智能落地的一个工具。

机器学习是人工智能的一个分支

深度学习是机器学习的一种方法，为了解决机器学习领域中图像识别等问题而提出的

数据分层：

数据采集层、数据存储层、数据分析层、数据展示

数据采集层

用户访问日志数据，数据格式：地区吗|用户ip|目的ip|流量……;数据采集方式：采用fatp方式长传服务器；上传时间：每小时上传上一小时的数据；小文件合并：通过shell完成文件合并；监控文件：JNotify

用户的安全日志数据：

当用户触犯电信部门制定的只读、违反国家法律法规

数据采集方式用：Socket---C++完成数据采集，先缓存到内存再到磁盘；

数据格式：加密码：加密形式 abc:79217979web

网卡配置：千兆或万超网卡配置

数据存储层：HDFS分布式文件系统

数据分析层：用Mapreduce、Impala\Spark

1、完成数据清洗（缺失字段处理、异常值处理等

2、使用MR和Redis进行交互完成地区码201和地区名字的转换

3、使用MR处理好的数据进一步加载到Hive中做处理

4、试用MR将数据入库到HBASE完成固定条件查询

5、给到Spark中实时查询

机器学习层：

机器学习位于大数据上层，完成的是在大数据的数据存储和数据计算之上，通过数据结合机器学习算法建构机器学习模型，利用模型对现实时间做出预测

数据展示：Oracle+SSM

大数据的4V特征：

1. 数据量大
2. 数据种类多：
   结构化数据（mysql）；
   非结构化数据（音频视频：HDFS/MR/HIVE);
   半结构化数据（XML/HTML: HDFS/MR/HIVE);
3. 速度快:
   增长速度快
   处理速度快（实时、离线）
4. 价值密度低
   价值密度=有价值的数据/ALL
   价值高
   机器学习算法解决问题

提升：

梯度提升

机器学习：使用计算机设计一个系统，使它能够根据提供的训练数据按照一定的方式来学习；随着训练次数的增加，该系统可以在性能上不断学习和改进；通过参数优化的学习模型，能够用于预测相关问题的输出。（强调学习 而不是专家系统）

有监督 

无监督 

强化学习（带反馈）

机器学习：数据清洗/特征选择；确定算法模型/参数优化；结果预测

不能解决：大数据存储/并行计算；做一个机器人

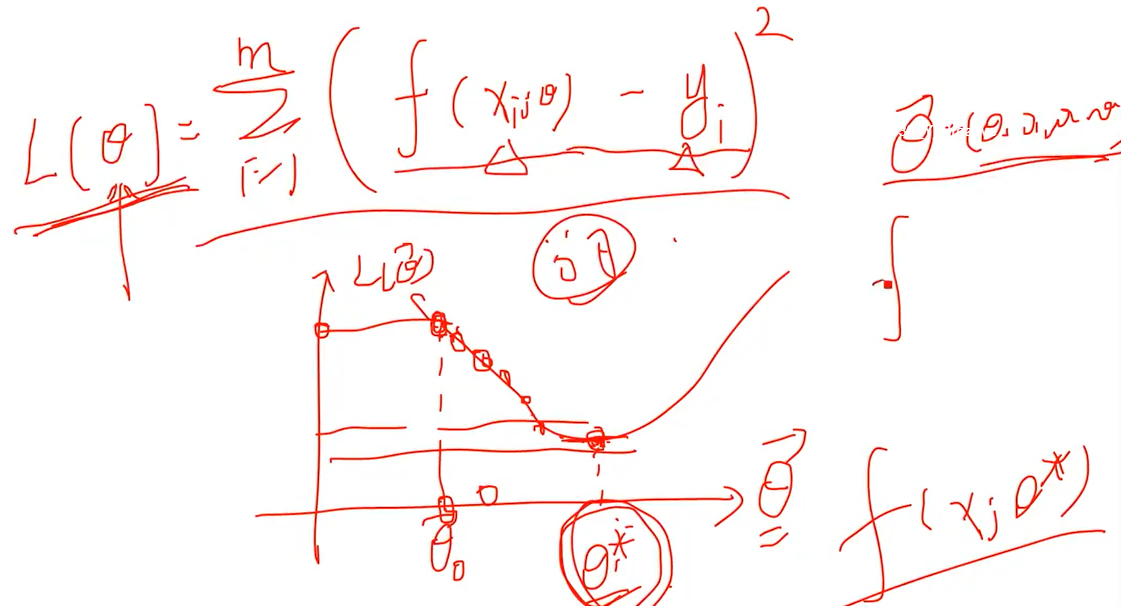
目标函数取最小称 损失函数

数据收集--->数据清洗----->特征工程----->数据建模

hessian矩阵 对称--》4>0 二阶行列式>0----》正定---->凸函数

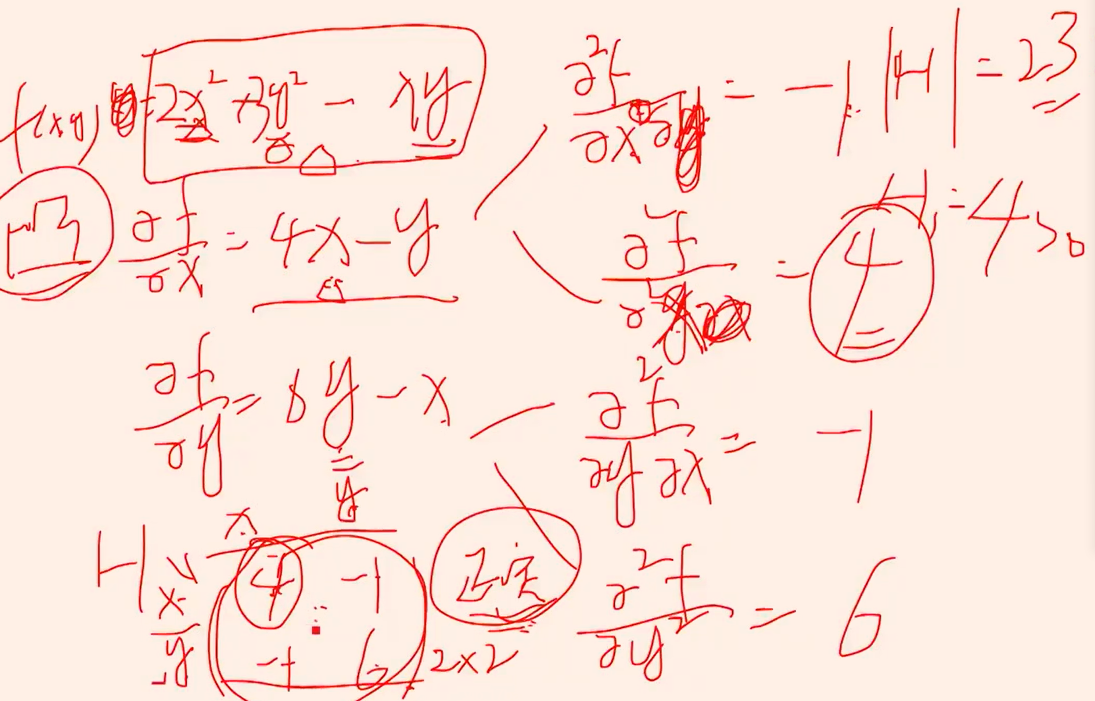
SST (总方差)= SSE() + SSR （残差平方和）

只有无偏估计下成立，否则 SST≥SSE+ SSR

局部加权

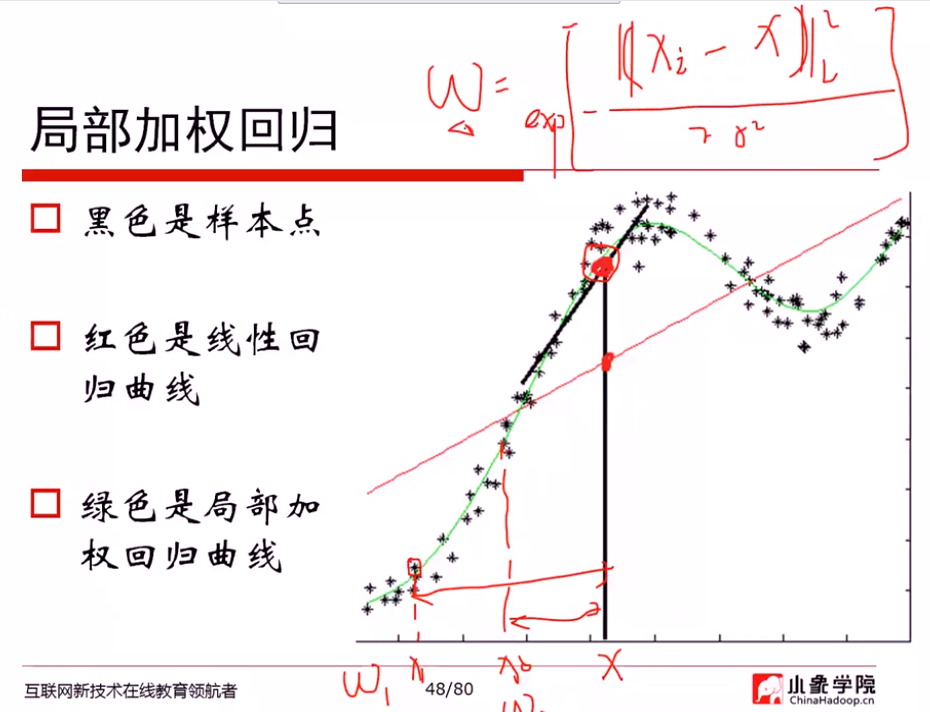
最重要的问题: 如何度量权重

Logistic回归

p(y|x:θ)  y=0, y=1时,写成上述密度函数形式

解法1: 从mle求解

极大似然估计的梯度上升算法，本质与梯度下降无区别，梯度上升取正梯度方向，同样设置步长a；梯度下降选取负梯度方向，

线性回归:  假定服从高斯分布，通过MLE进行估计

logistics回归: 假定服从二项分布，通过MLE进行估计

如果都进行梯度下降法估计，会发现求解的方式都是一样的

广义线性模型的定义: 因变量不服从正态分布，且因变量与自变量不存在线性关系；广义就是要找一个非线性的关系f，使得转换后更接近因变量的分布

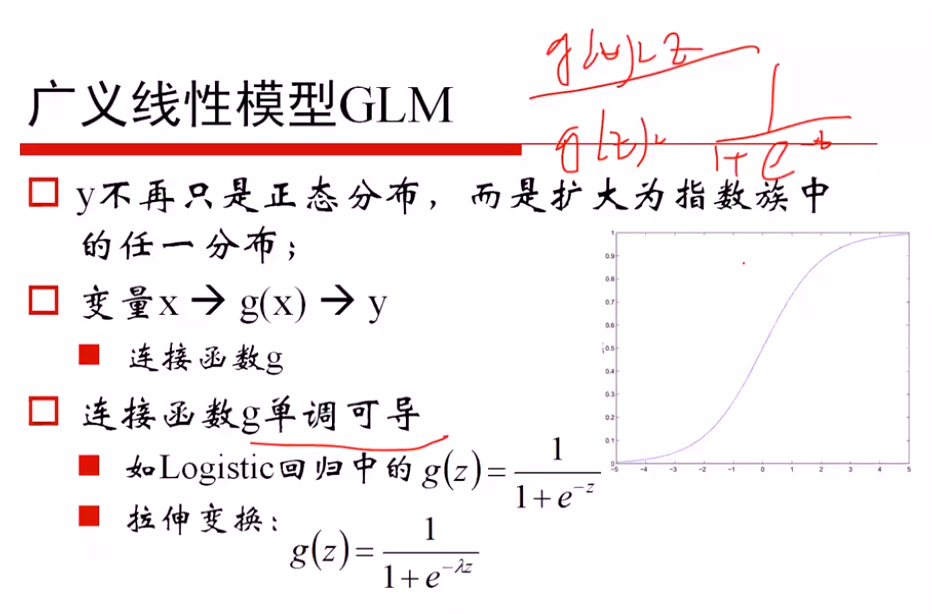
证明是一个广义的线性模型:

对数线性模型:

从对数模型理解 logistics函数

一方面: 从 ln(p/(1-p)) = θx 推导出 p = logistics函数，说明希望对数模型是线性的，从而推导出概率可以用logistics函数表示

另一方面: 从 p=logistics函数 + ln(p/(1-p))对数模型，推导出对数模型是线性的θTx

广义线性模型  → 相似的梯度下降方法

解法2: 从损失函数进行求解

(1)对 -1, 1转换为0, 1  进行(yi+1)/2...

softmax回归

鸢尾花数据

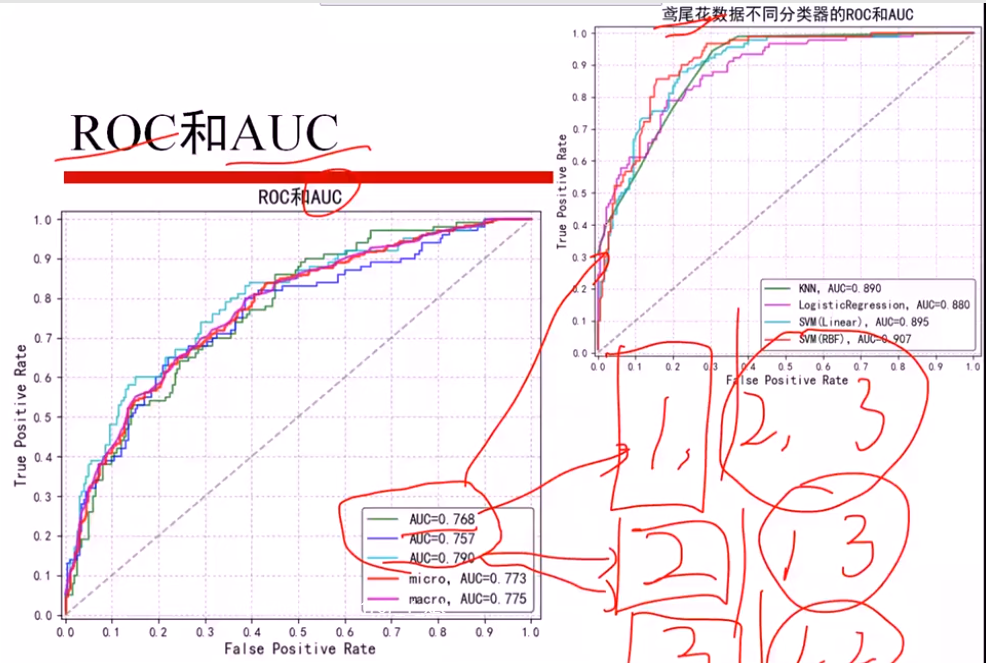
分为三个 二分类问题，算出三个AUCi值

micro: 直接算三个平均AUCi，得出AUC

macro: 总体加和，当作一个AUC计算

1. 线性回归

• 极大似然估计解释最小二乘

假设: 误差ξ服从高斯分布(0, δ)

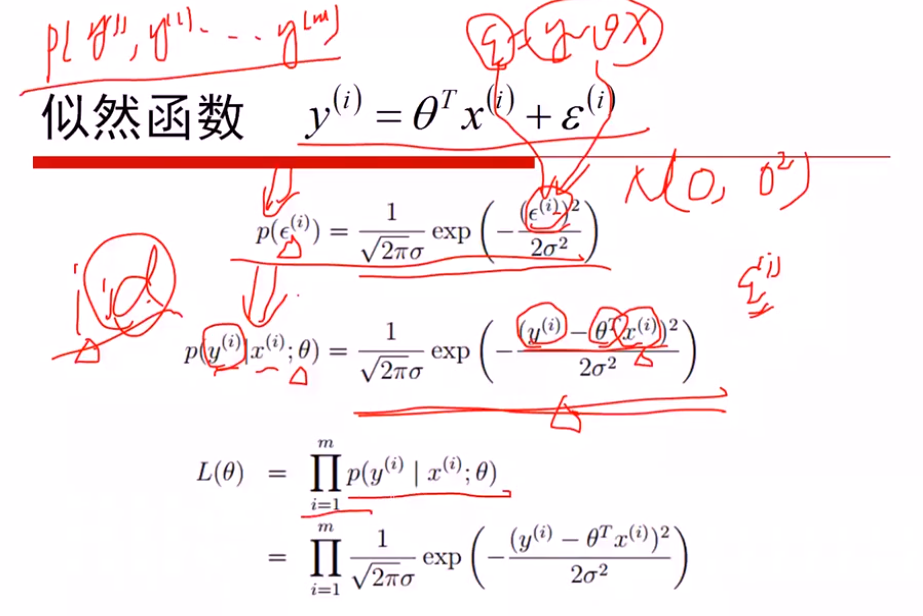
①最大化似然函数，对l(θ)进行简化

max l(θ)  等价于 min(J(θ))

• 1 最小二乘的矩阵推导

注意:

(1)是关于θ的函数，最大化θ参数

(2)J(θ)是一个xTx的凸函数，因为xTx是半正定的，开口向上，xTxθTθ就是关于θ的开口向上的二次函数

• 线性回归复杂度惩罚因子

（1）L2正则，进行对θ惩罚 -- Ridge回归

         L1正则，  --  Lasso回归

• 解释为什么L1有特征选择能力:

1 拉格朗日角度进行解释

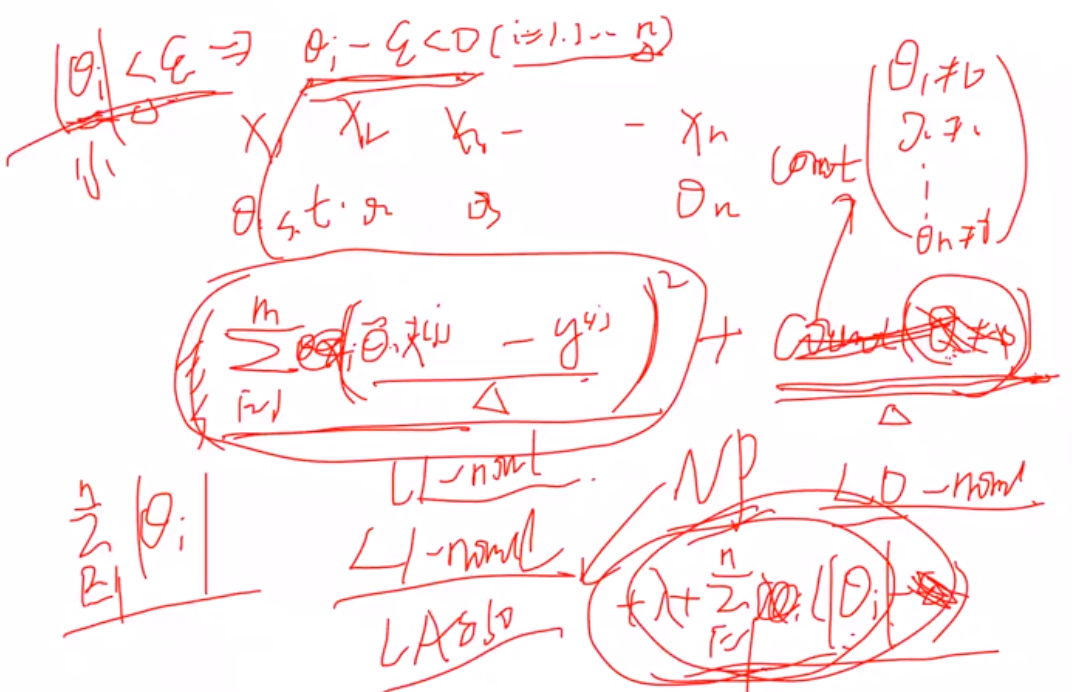
（1） 原本的目标: 希望θ=0就计0，不等于0就计为1，惩罚θ>0时候的数目，但是由于是无解的，因此用L1范数进行近似

推导看手稿:

2 几何解释:

L1约束使得某一个wi是0，稀疏约束

L2使得两个wi都比较小，约束

• L1正则不可导如何解决?

(1)坐标轴下降法

(2)近端梯度近似法...  其余还有很多

• 2 广义逆矩阵求解（伪逆）

（1）当x可逆， θx =y可以直接进行求解，不用进行目标函数最小化求解，因此可以利用SVD进行奇异值分解，求出伪逆矩阵后进行求解 

• 3 梯度下降法求解

1. Logistics 回归
2. 多分类softmax回归
3. 技术:

• 梯度下降
• 最大似然估计
• 特征选择

1. 1 贝叶斯, MLE的思想

假设1：p(Ai) 概率相似

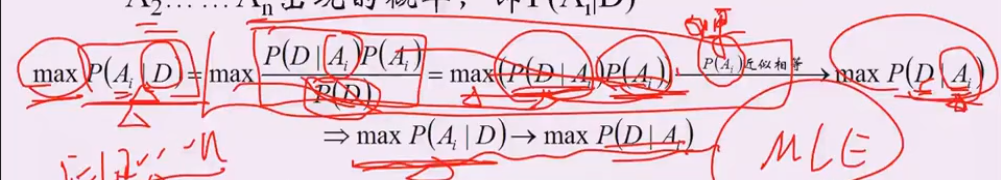
P（D|Ai)： 给定结论Ai下， 这个数据以多大的概率产生。 可以理解为x1..xn是未知的数据参数，θi是已知的参数，能够使  p(x1..xn|θi)最大的参数θi，就是我们想要估计的参数， 这里xi对应D，Ai对应参数θ

1. 2 赔率分析

公平赔率； y = 1/p   y是赔率，p是赢的概率

赔率公式    y =a/p

计算庄家盈亏:

10.5% = 0.21 a / 2a

1. 3 模糊查询与替换

2 PCA

2.1 原理

①求协方差矩阵

② 特征值排序

③ 方差最大的就认为是主要的方向，其中特征向量相互垂直，每一个特征向量就是一个方向，Aμi的方差最大，就认为是最主要的投影方向

①假定样本已经作了中心化，所以忽略均值E

Q 为什么特征值最大 等价于 求方差最大？

PCA中希望投影的方差最大，认为得到的信息最多。

目标函数: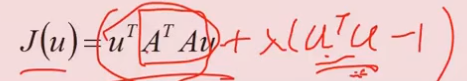

加上等式约束  μTμ=1， 根据拉格朗日求解，

aJ/aμ = 2ATAμ +2λμ = 0 ,求得λ就是 ATA的特征值。

因此，方差最大 等价于 最大特征值

2.2 过拟合问题

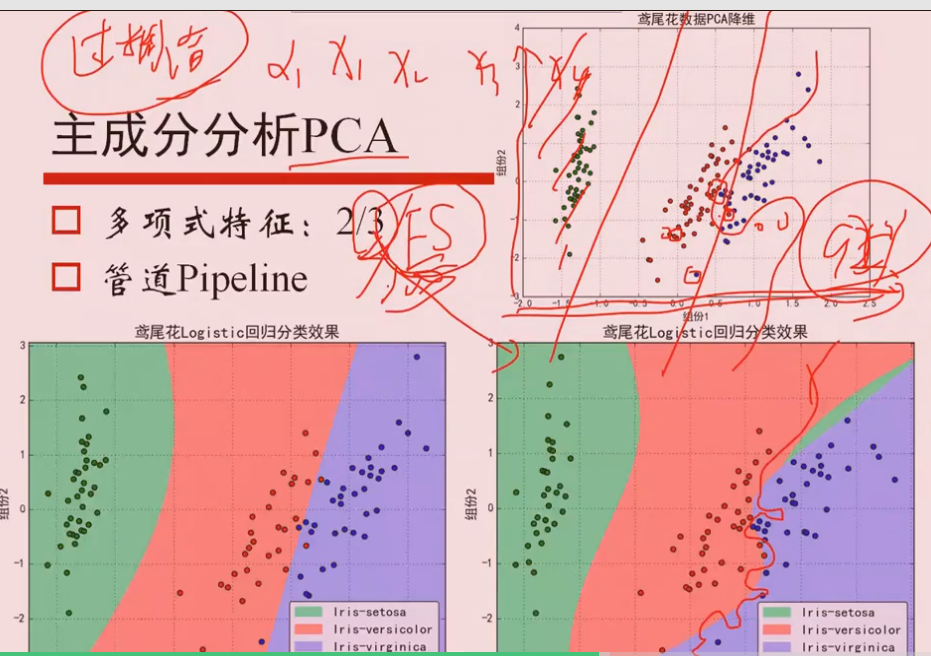
使用高阶的特征x1^2, x2^2...，特征过多，虽然会得到弯曲的曲线进行分离，但是很有可能产生过拟合问题

决策树不需要做one-hot编码

6.1 Prime

计算素数:  

fliter(函数, x): 把数字放入x中，结果输出

模型选择：了解每个模型；

EM算法无监督聚类燕尾花

GMM与图片分析

图像卷积

crawler 爬数据

# 回归

## 一、线性回归

- 离散型数据：分类

- 连续型数据：回归

### y=kx+b

### 多个变量的情况

# 数据清洗和特征选择

## fuzzeywuzzy模糊查询

- 任何一次插入，修改和删除算作一次过程+1