O 来自 order 大写：以多项式的最大的次项的次数 大O(n) 表示 f(x) =O(g(x))  f(x)的阶与g(x)的阶相同

小写O f(x)=o(g(x))  f(x)的阶小于g(x)的阶

梯度下降法

误差来源于两个——一个是bias，还有一个是variance。出现bias是由于开始就没有瞄准靶心；出现vaiance是由于瞄准了靶心，但是发射的时候出现了偏离。我们的目标是低bias和低variance。

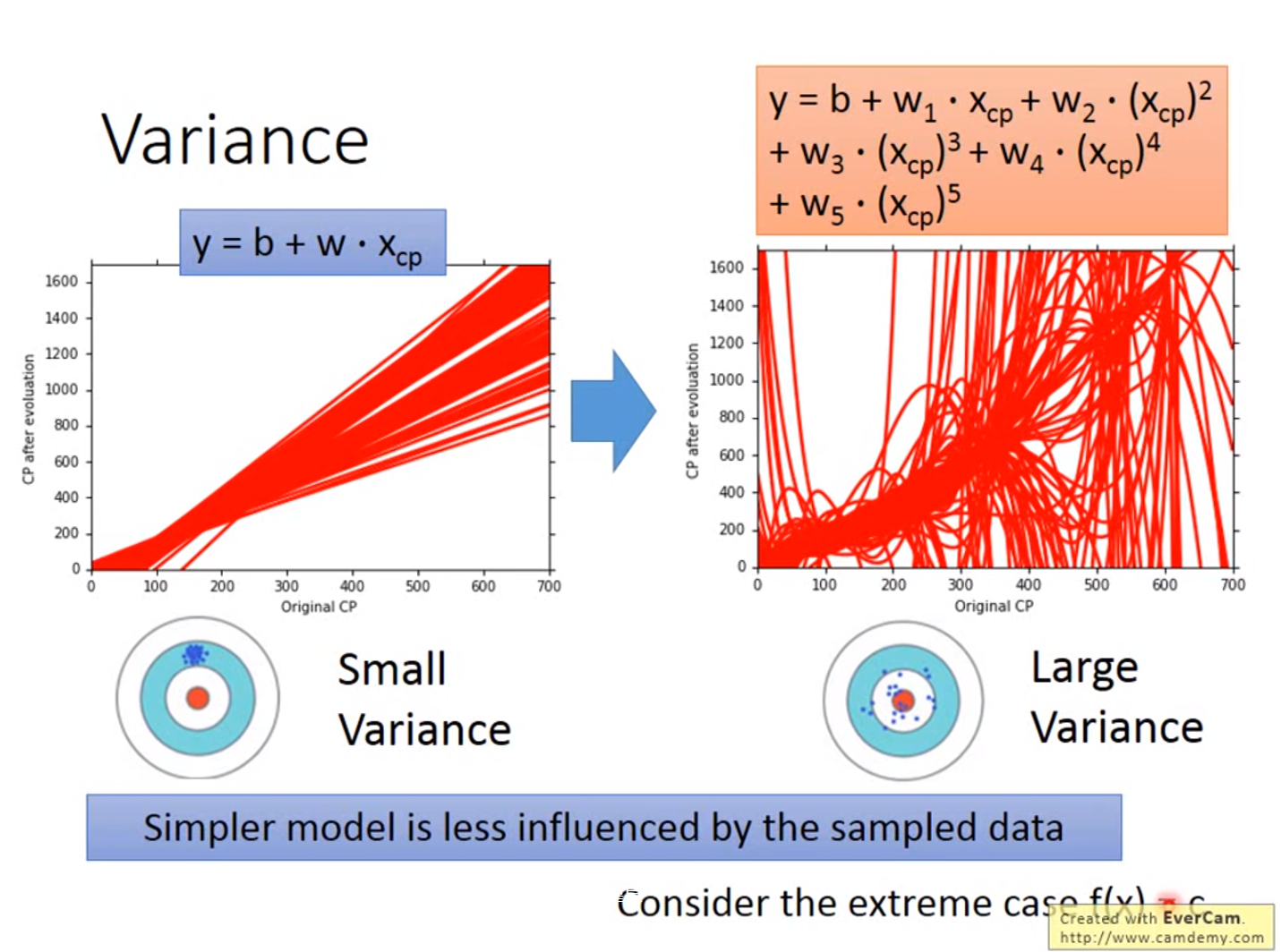
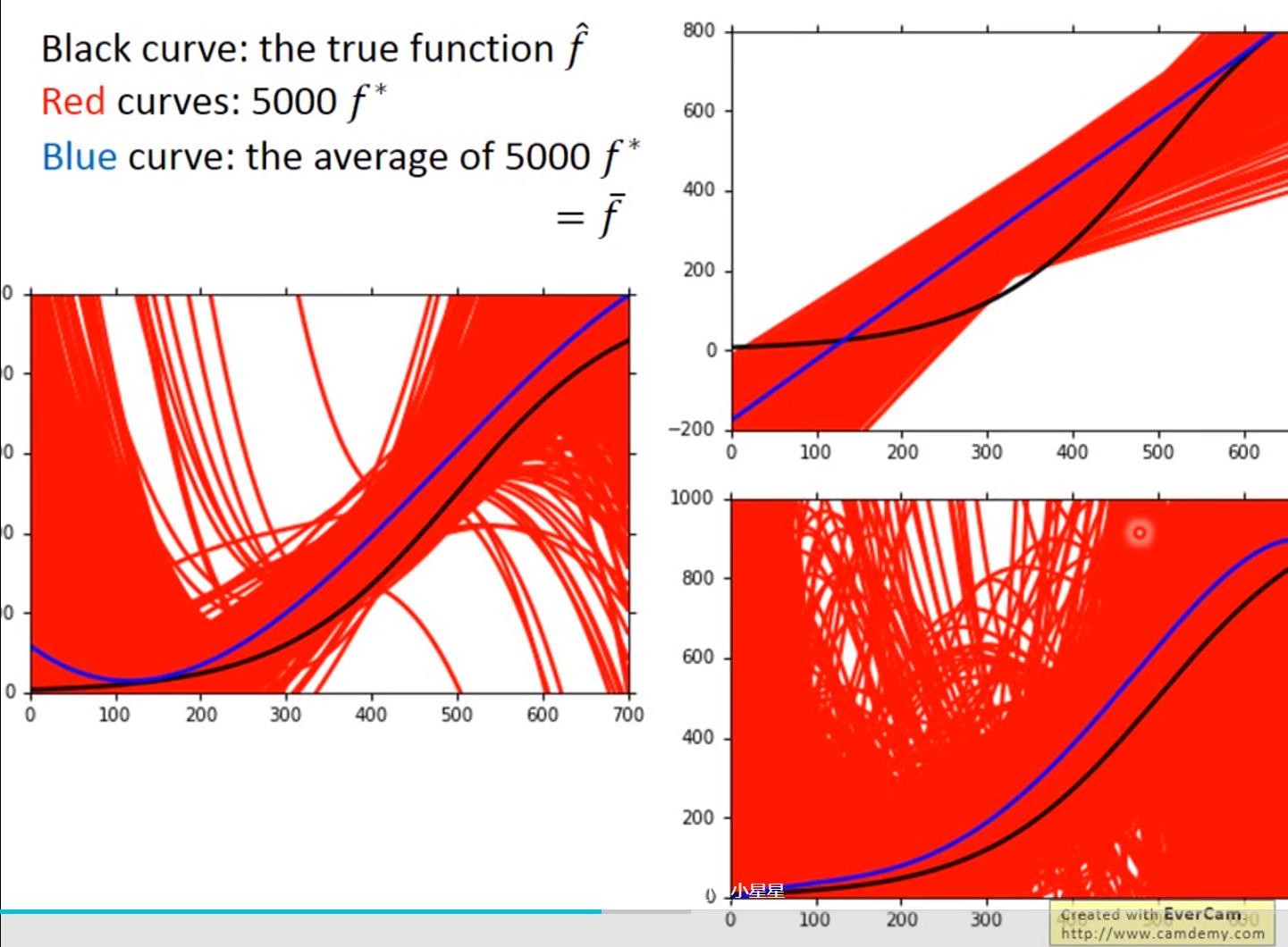
红色的部分是分别在考虑输入值一次方、三次方和五次方函数进行5000次实验的结果，蓝色的线条是将5000次实验结果进行平均即结果

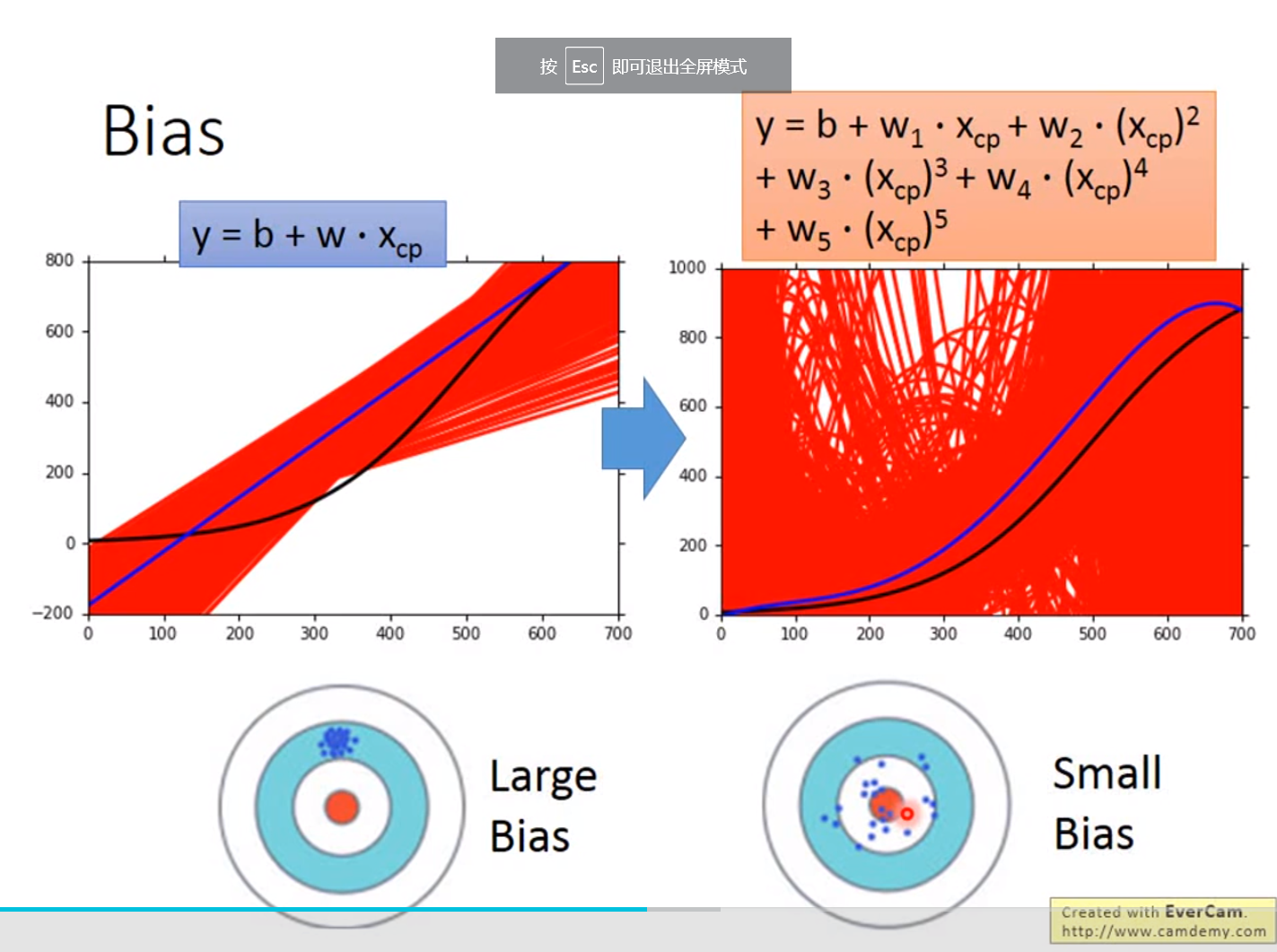
越简单的模型，bias越大，variance比较小；反之，模型越复杂，variance越大，但是平均值却比较接近于期望值

bias较大的情况，问题出现在underfitting；

variance较大的情况，问题出现在overfitting

Diagnosis：

(1)当模型不能拟合训练集时，我们有较大的bias；

(2)当模型可以集合训练集，但是在测试集上出现了较大的损失值，则很大可能上有较大的variance

for bias, redesign模型：
（1）add more feature as input

（2）a more complex model

for variance

（1）more data（增加每次实验的样本量）

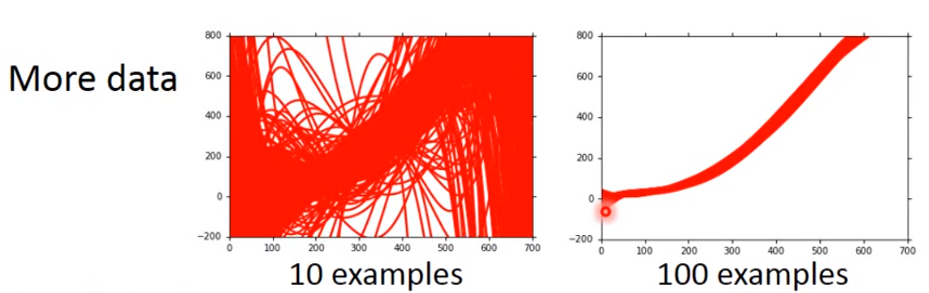
（2）Regularization我们希望曲线越平缓越好

伤害：只包含了比较平滑的曲线，在取值上产生了较大的bias

model selection：

我们想要找到尽可能小的bias和variance来得到最小的损失值

Regression回归

1、应用场景

（1）Stock Market Forecast

（2）Self-driving Car

（3）Recommendation

2、步骤

（1）给一个Model

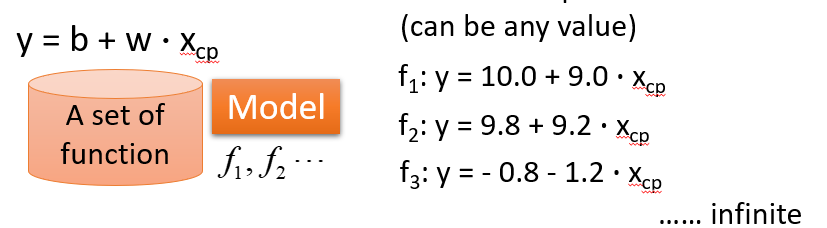
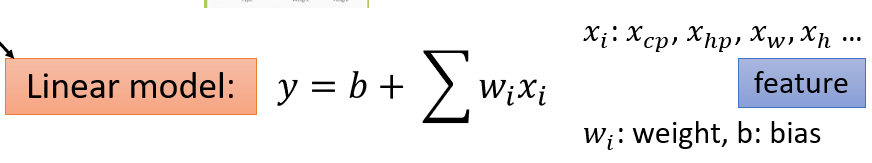
（2）Goodness of Function（函数优度）

输入：a function一个函数

输出：loss funchtion——how bad it is 

Pick the “Best”Function

（3）Gradient Descent

梯度下降：初试化w和b这两个参数，不断迭代更新，知道找到最优解，也就是使损失值达到最小的参数值

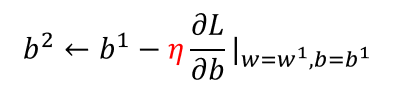
在线性回归里，是不需要担心找不到全局最优解的，因为其三维图形是一圈一圈的等高线，不管从哪个方向都可以找到最优解

how's the results？

训练的目的是损失值最小，但是通过训练集得到的损失值是比测试集得到的损失值小的，为了减少误差，我们需要改进模型——引入了二次方、三侧方和四次方的函数

overfitting——更复杂的模型会得到更不好的结果，所以模型并不是越复杂越好。

what are the hidden factors——pokemon的物种会影响他们值

根据不同的输入值，对不同的物种设置不同 的权重，此时仅设置了输入值的一次方，还可以考虑输入值的二次方函数

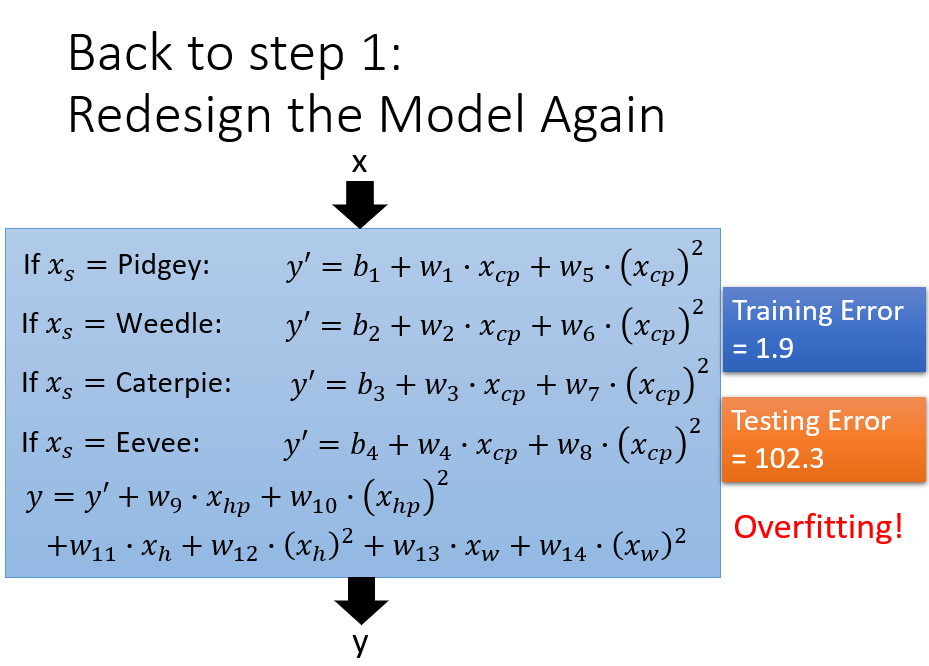
产生了过拟合的结果

设置较为平缓的曲线，由于w的值大于零小于1，当其越接近于0，结果是越为平缓的，前面的系数越大，代表我们越考虑smooth，越可以较多得关注参数w本身的值

连续[2:5,1:4]跳跃[[2,1],[3,5]]

1. 集合
2. 元素
3. 描述方式
4. ​​​​​​​子集
5.  

让机器学习程序替换手动步骤，减少企业的成本，也提高企业的效率

真是听过讲的最烂的，重点yong'yuan'tiao'guo

# Machine learning

- make decisions

- go right/left 

- increse/decrease

# 为什么使用tensorflow

- GPU加速 比cpu快很多

- 自动求导

- 神经网络API

> 给与cpu和gpu一个热身的时间：warm-up

数据分析的流程:

1. 提出问题
2. 准备数据
3. 分析数据
4. 获得结论
5. 成果可视化

### 对于LightGBM：又轻又快

在不降低准确率的前提下，速度提升了10倍左右，占用内存下降了3倍左右。因为它是基于决策树算法的，它采用最优的==叶明智==策略分裂叶子节点，然而它的提升算法分裂树一般采用的是深度方向或者水平明智。因此，当增长到相同的叶子节点，叶明智算法比水平-wise算法减少更多得损失。因此导致更高的精度。

J_\theta=-l(\theta)

### logistic函数：通过回归进行分类

### logistic回归的过程

- 1) 找到一个合适的预测函数，一般表示为h函数，该函数就是我们需要找的分类函数，它用来预测输入数据的判断结果。这个过程是非常关键的，需要对数据有一定的了解和分析，知道或者猜测预测函数的大概形式，比如是线性函数还是非线性函数。

- 2）构造一个loss损失函数，该函数表示预测的输出与训练数据类别之间的偏差。可以是二者之间的差或者是其他的形式。综合考虑所有训练数据的损失，将loss求和或者求平均，记为J(theta)函数，表示所有训练数据预测值与实际类别的偏差。

- 3）显然，J函数的值越小表示预测函数越准确。所以这一步需要做的是找到J函数的最小值。找到最小值有不同的方法。如梯度下降法。

# 线性回归

## 方程y=Ax

## 最小二乘法（平方）Least Squares Method

\sum_(n=1)^N（y-y_i）^2

w\hat=(\pmb{X^T}\pmb{X})^-1\pmb{X^T}y

> 让平方误差最小

集成算法

- bagging：套袋法

- boosting：提升算法：增大错误样本的权重同时减小正确样本的权重。与bagging对比boosting可以同时降低偏差和方差，而bagging只能降低模型的方差。但boosting更加容易过拟合。

- 随机森林：应用bagging和多颗决策树

- 梯度提升树

- adaboost：

> adaboost算法与boost算法不同，它是使用整个训练集来训练弱学习器，其中训练样本在每次迭代的过程中都会重新被赋予一个权重，在上一个弱学习器错误的基础熵进行学习来构建一个更加强大的分类器。

# sklearn学习

## 介绍

-  数据分析和数据挖掘

- 用python进行机器学习

> 数据分析和数据挖掘==机器学习==人工智能

## 分类

- classification

- regression

- clustring

- dimensionality reduction

- model selection

- preprocessing

# 非监督学习

## k-means （聚类）

> 聚类做在分类之前