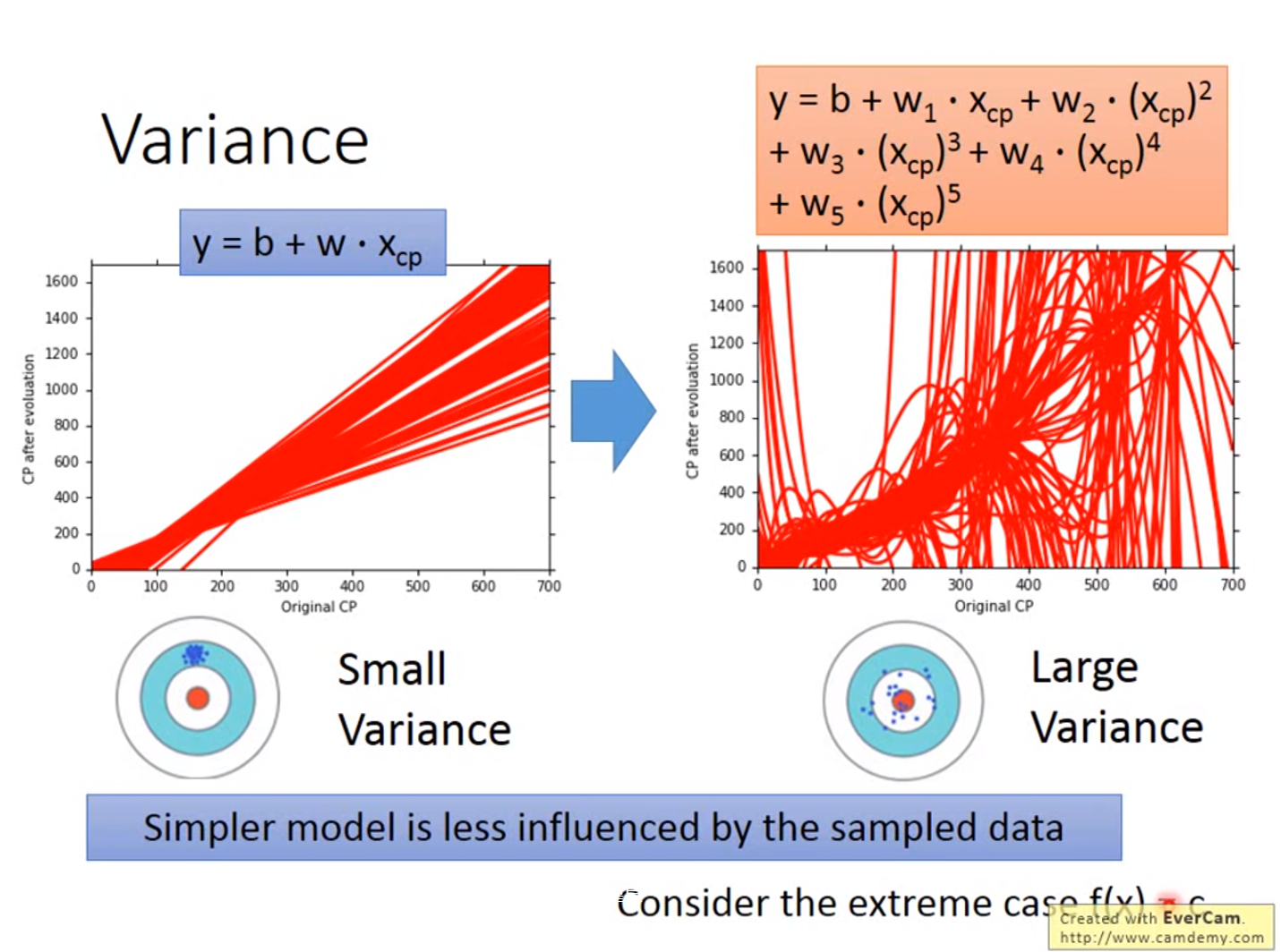
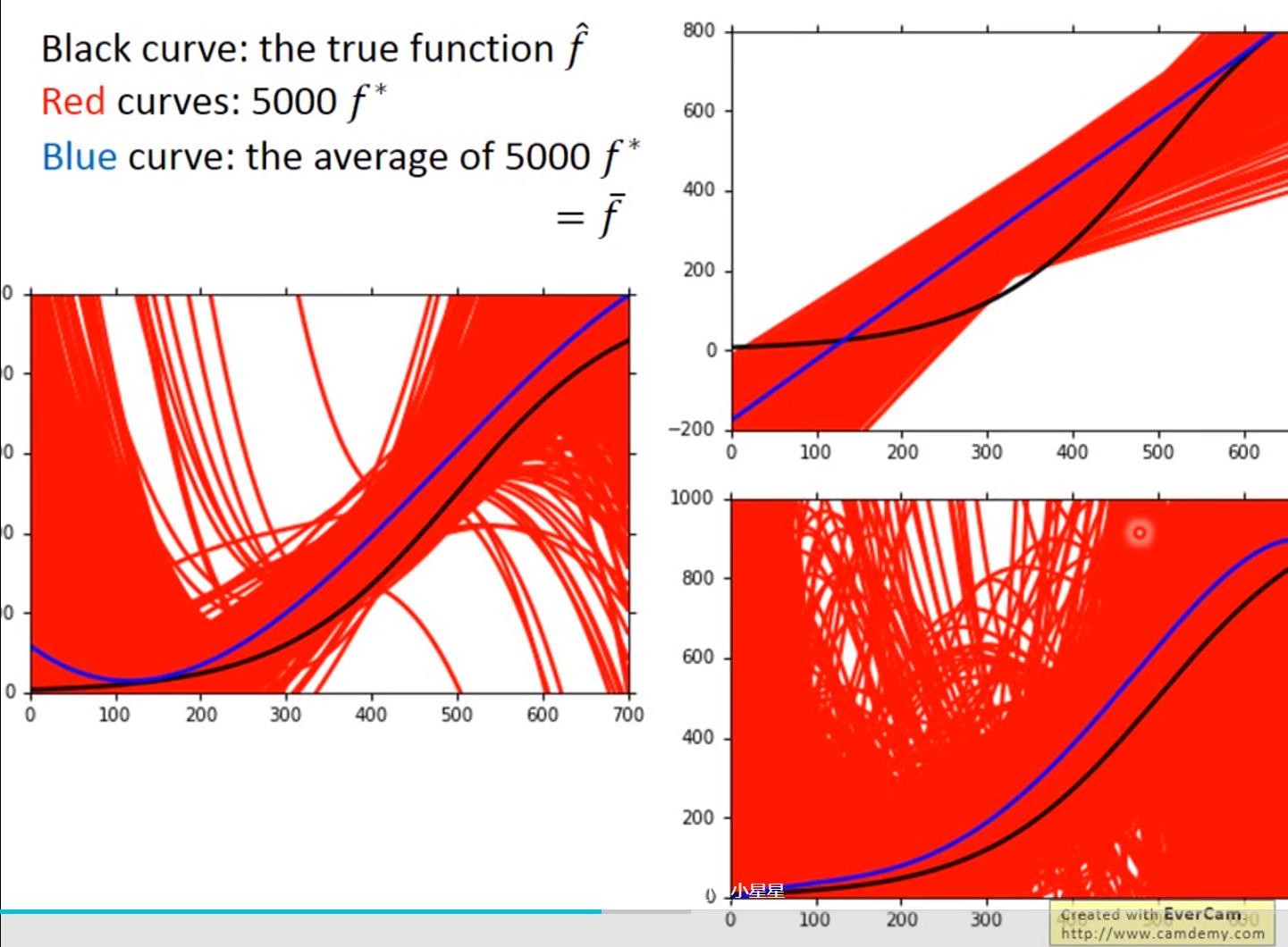
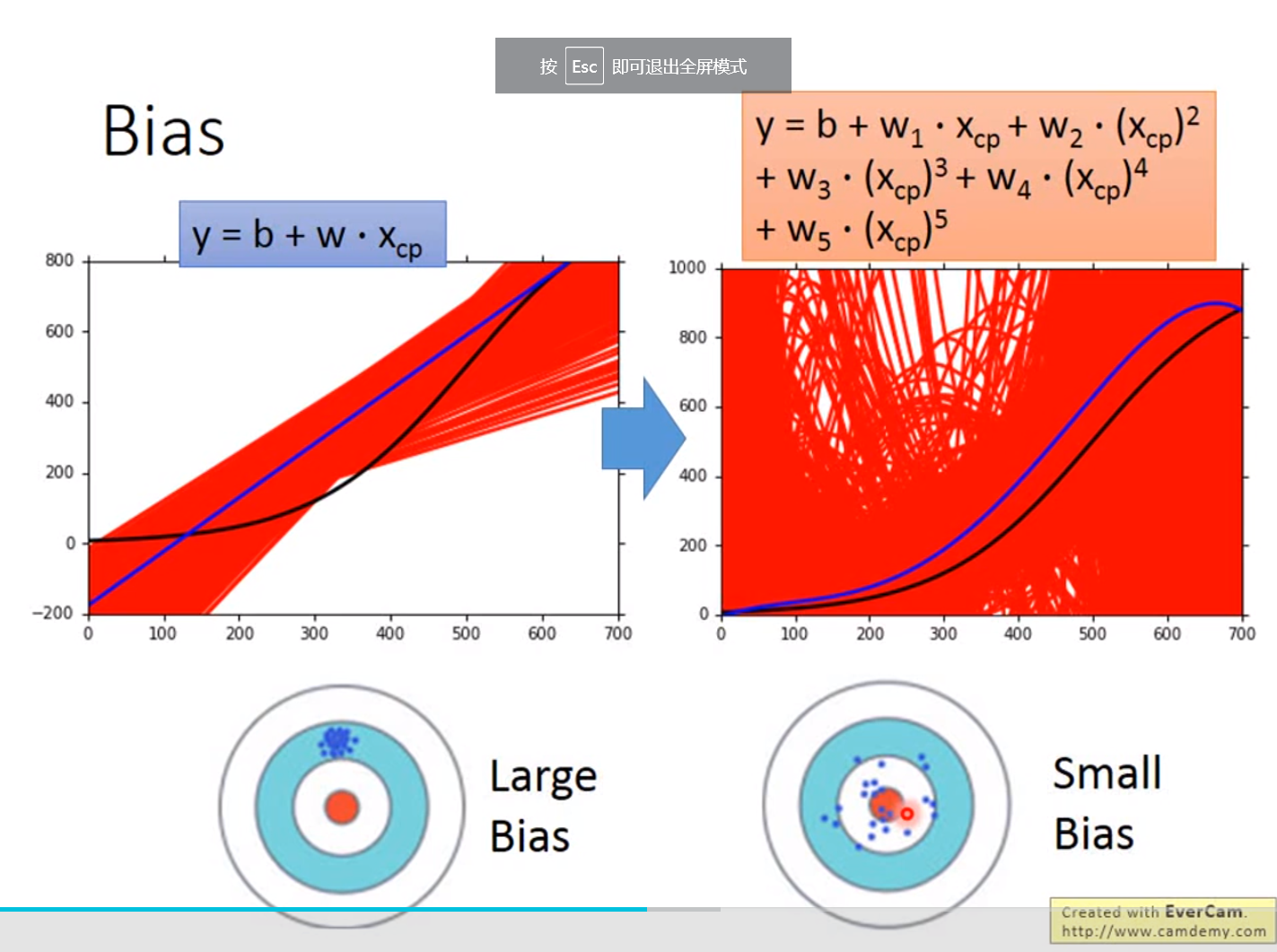
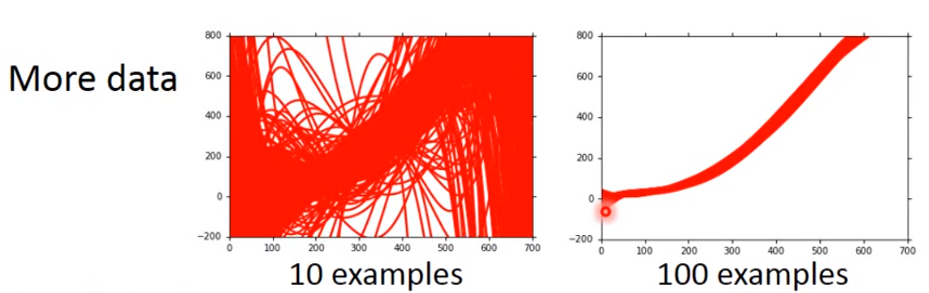
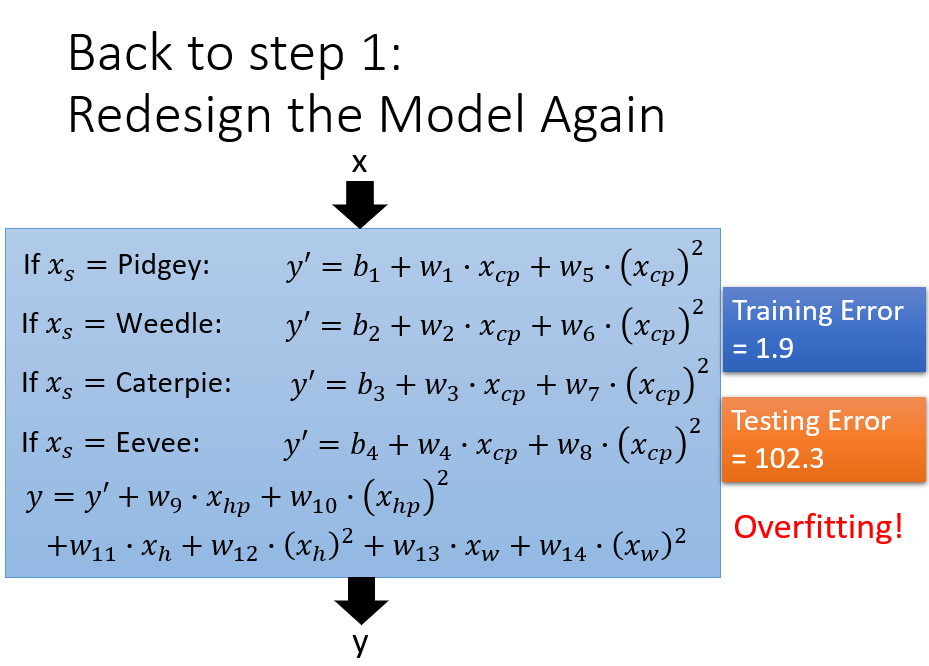
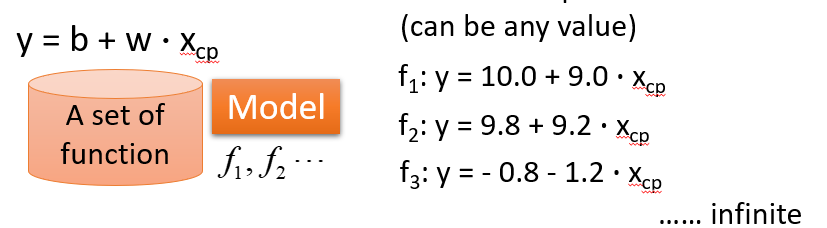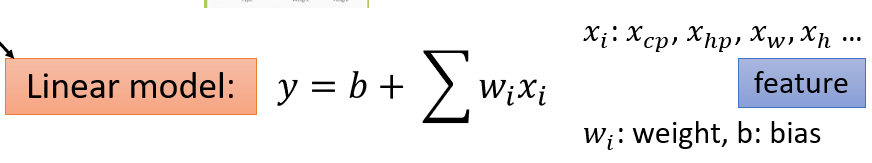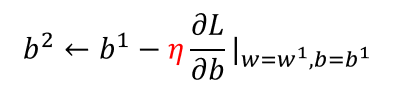Gradient Descent

Gradient：loss损失函数等高线的发现方向

需要注意的是：learning rate 需要设置合理

如果learning rate很小，loss下降的很慢；

如果learning rate表达大，可能卡住，找不到loss的极小值；

如果learning rate非常大，loss有可能越来越大

只有当learning rate 刚刚好的时候，我们才能得到loss的极小值

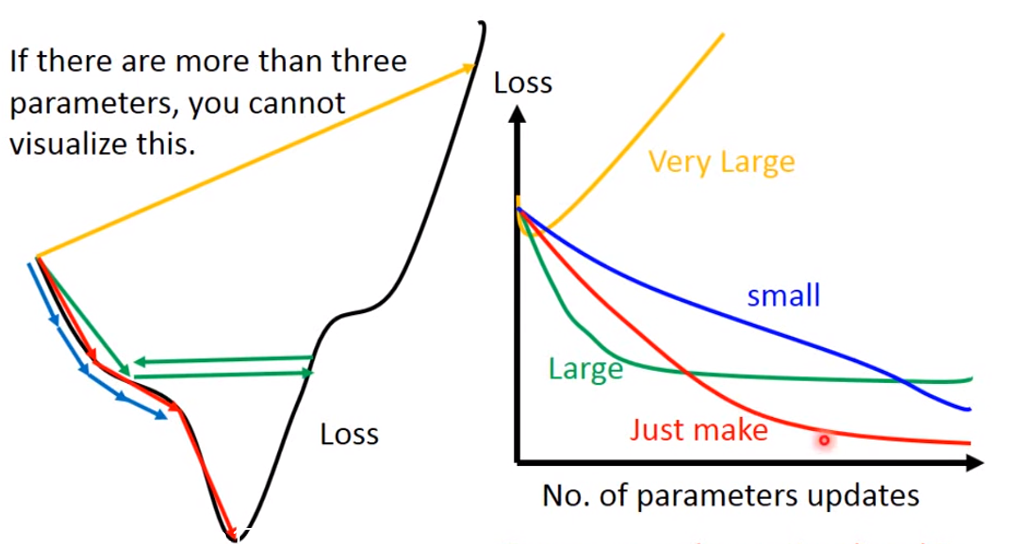
Adagrad

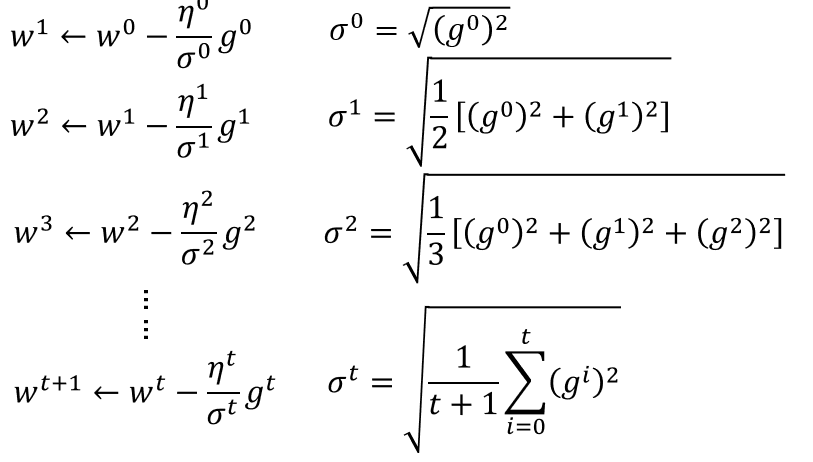
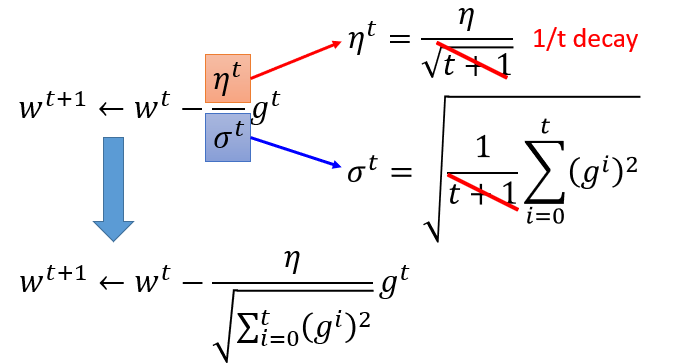
有个矛盾点是，对于gt来说，梯度越大，w参数应该下降得越快，但是分母上也有g的和，分母越大，w参数值下降得越小，这里应该如何理解？

对于2次函数来说，可以直观的看出Adagrad的优势

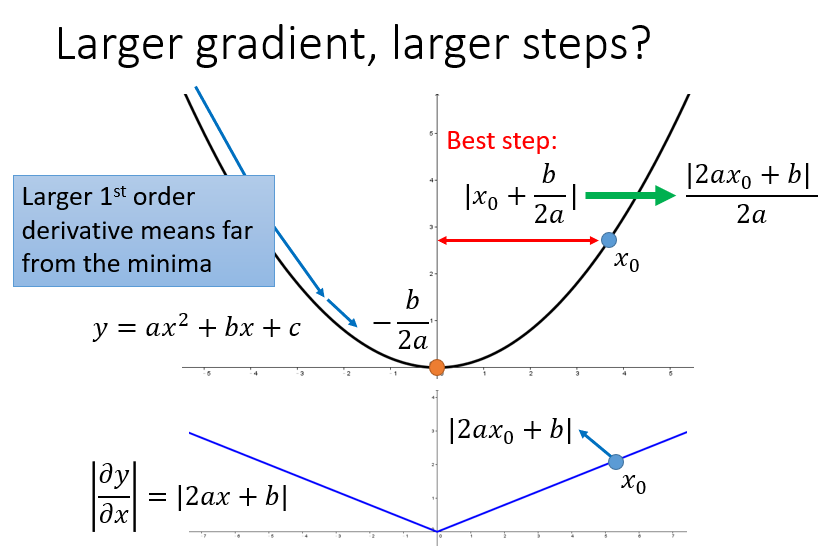
最好的步长是一阶导的绝对值除以二阶导的值

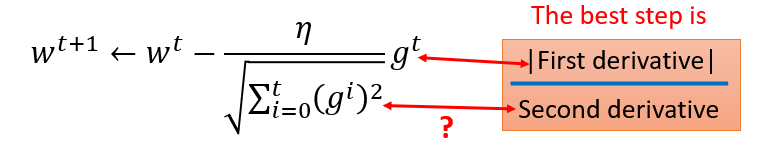
这里的分母虽然是一阶导的绝对值的和，但在一定程度上可以看出二阶导的大小来

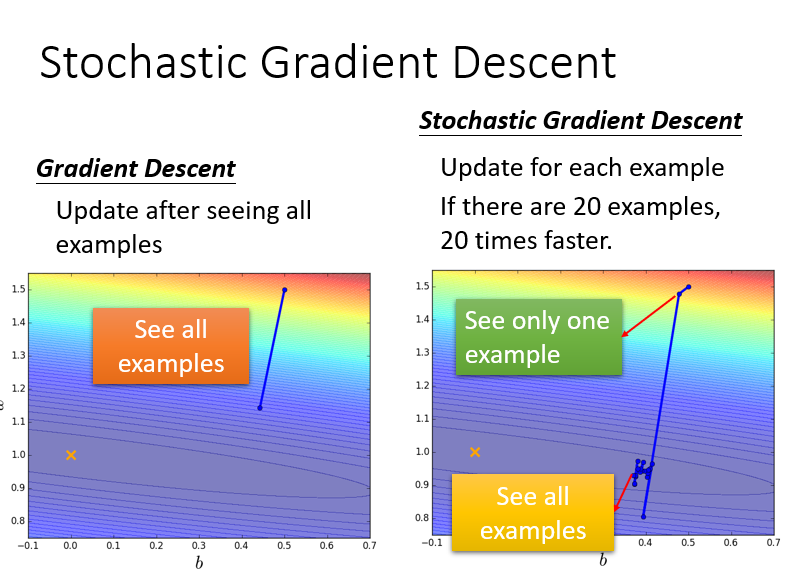
Stochastic Gradient Descent

只看一个example，只考虑一个点的参数值（其实没听懂）

Feature Scaling

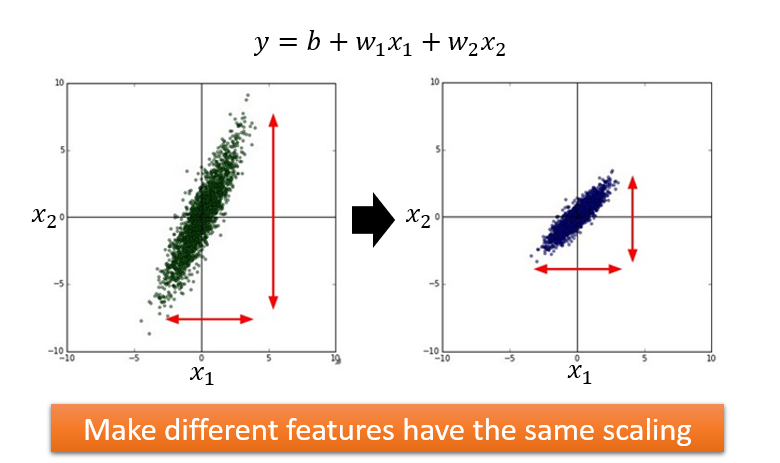
做法：

梯度下降背后的数学原理

泰勒定理：

多元的情况下：

误差来源于两个——一个是bias，还有一个是variance。出现bias是由于开始就没有瞄准靶心；出现vaiance是由于瞄准了靶心，但是发射的时候出现了偏离。我们的目标是低bias和低variance。

红色的部分是分别在考虑输入值一次方、三次方和五次方函数进行5000次实验的结果，蓝色的线条是将5000次实验结果进行平均即结果

越简单的模型，bias越大，variance比较小；反之，模型越复杂，variance越大，但是平均值却比较接近于期望值

bias较大的情况，问题出现在underfitting；

variance较大的情况，问题出现在overfitting

Diagnosis：

(1)当模型不能拟合训练集时，我们有较大的bias；

(2)当模型可以集合训练集，但是在测试集上出现了较大的损失值，则很大可能上有较大的variance

for bias, redesign模型：
（1）add more feature as input

（2）a more complex model

for variance

（1）more data（增加每次实验的样本量）

（2）Regularization我们希望曲线越平缓越好

伤害：只包含了比较平滑的曲线，在取值上产生了较大的bias

model selection：

我们想要找到尽可能小的bias和variance来得到最小的损失值

Regression回归

1、应用场景

（1）Stock Market Forecast

（2）Self-driving Car

（3）Recommendation

2、步骤

（1）给一个Model

（2）Goodness of Function（函数优度）

输入：a function一个函数

输出：loss funchtion——how bad it is 

Pick the “Best”Function

（3）Gradient Descent

梯度下降：初试化w和b这两个参数，不断迭代更新，知道找到最优解，也就是使损失值达到最小的参数值

在线性回归里，是不需要担心找不到全局最优解的，因为其三维图形是一圈一圈的等高线，不管从哪个方向都可以找到最优解

how's the results？

训练的目的是损失值最小，但是通过训练集得到的损失值是比测试集得到的损失值小的，为了减少误差，我们需要改进模型——引入了二次方、三侧方和四次方的函数

overfitting——更复杂的模型会得到更不好的结果，所以模型并不是越复杂越好。

what are the hidden factors——pokemon的物种会影响他们值

根据不同的输入值，对不同的物种设置不同 的权重，此时仅设置了输入值的一次方，还可以考虑输入值的二次方函数

产生了过拟合的结果

设置较为平缓的曲线，由于w的值大于零小于1，当其越接近于0，结果是越为平缓的，前面的系数越大，代表我们越考虑smooth，越可以较多得关注参数w本身的值