降维算法

一、维度概述

1、对数组和Series，shape中返回几个数字就是几维，几个方括号就是几维

2、特征矩阵，DataFrame，几个特征就是几维，对应图中几个坐标轴，降维降的是特征数量

二、降维算法decomposition.PCA：主成分分析

1、PCA使用的信息量衡量指标为样本方差，越大，该特征带有信息量越多。

2、降维后找到的每个新特征向量叫“主成分”，新特征没有可读性，属于特征创造。线性回归不适合使用PCA。

3、重要参数

三、降维算法SVD

降维算法计算量很大

PCA使用的信息量衡量指标，就是样本方差，又称可解释性方 差，方差越大，特征所带的信息量越多。

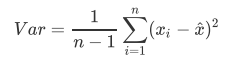
下去补补数学知识吧···

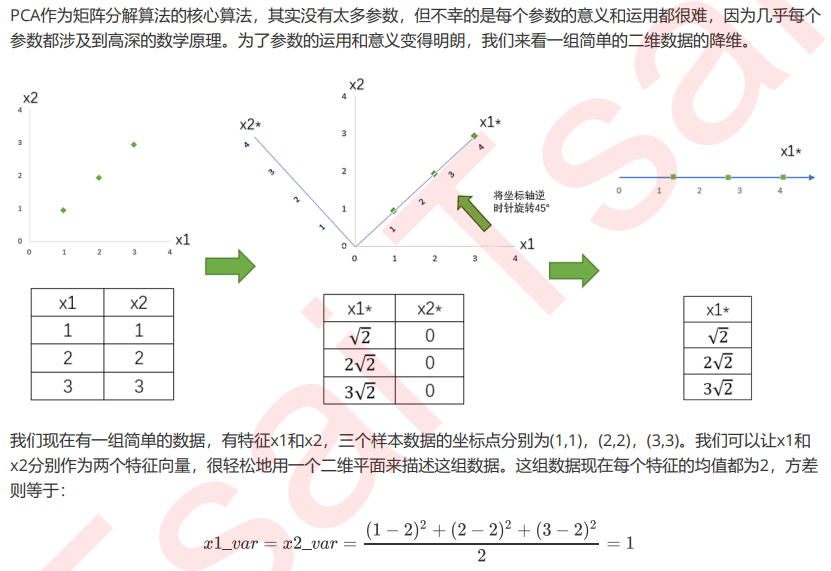
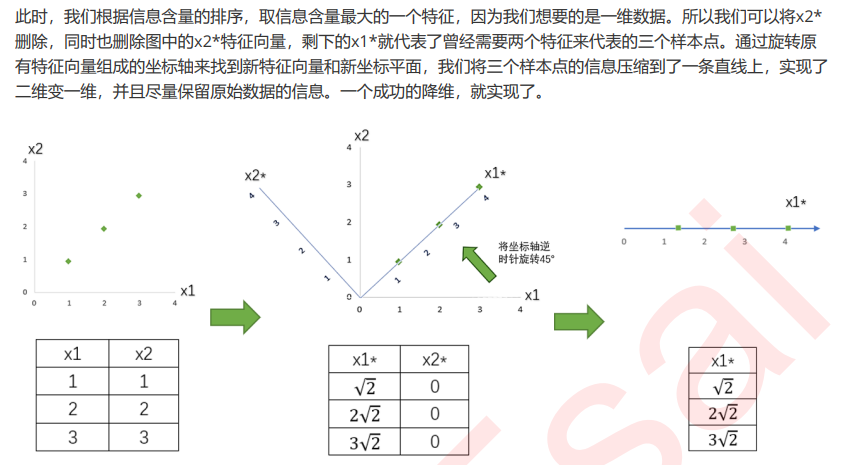
将为过程的主要步骤如下：

思考：PCA和特征选择技术都是特征工程的一部分，它们有什么不同？

特征工程中有三种方式：特征提取，特征创造和特征选择。仔细观察上面的降维例子和上周我们讲解过的特征 选择，你发现有什么不同了吗?

特征选择是从已存在的特征中选取携带信息最多的，选完之后的特征依然具有可解释性，我们依然知道这个特 征在原数据的哪个位置，代表着原数据上的什么含义。

而PCA，是将已存在的特征进行压缩，降维完毕后的特征不是原本的特征矩阵中的任何一个特征，而是通过某 些方式组合起来的新特征。通常来说，在新的特征矩阵生成之前，我们无法知晓PCA都建立了怎样的新特征向 量，新特征矩阵生成之后也不具有可读性，我们无法判断新特征矩阵的特征是从原数据中的什么特征组合而 来，新特征虽然带有原始数据的信息，却已经不是原数据上代表着的含义了。以PCA为代表的降维算法因此是 特征创造（feature creation，或feature construction）的一种。

可以想见，PCA一般不适用于探索特征和标签之间的关系的模型（如线性回归），因为无法解释的新特征和标 签之间的关系不具有意义。在线性回归模型中，我们使用特征选择。