SST (总方差)= SSE() + SSR （残差平方和）

只有无偏估计下成立，否则 SST≥SSE+ SSR

局部加权

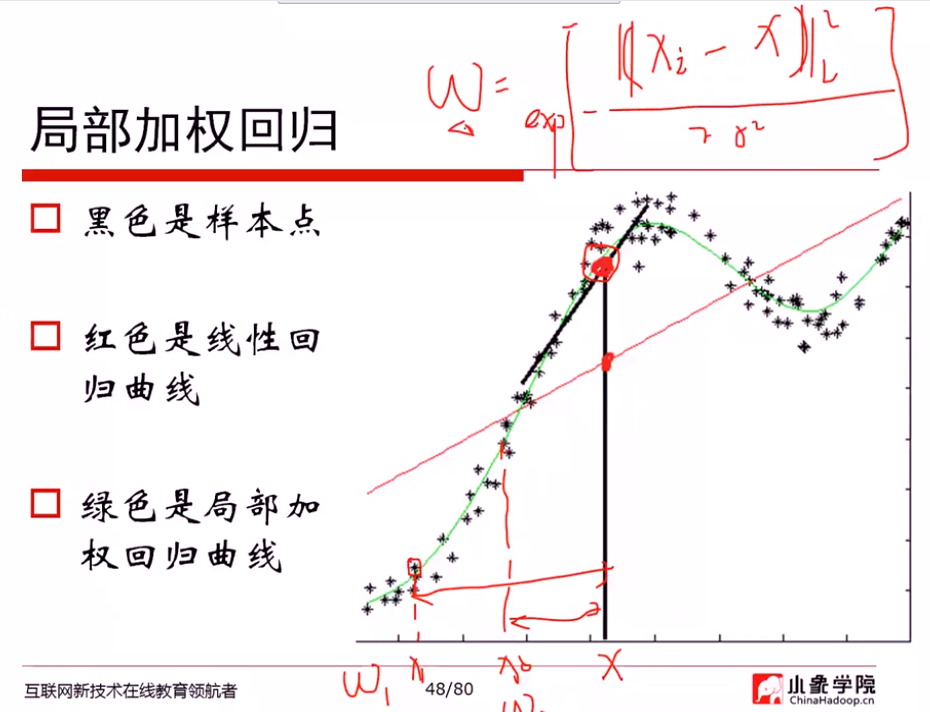
最重要的问题: 如何度量权重

Logistic回归

p(y|x:θ)  y=0, y=1时,写成上述密度函数形式

解法1: 从mle求解

极大似然估计的梯度上升算法，本质与梯度下降无区别，梯度上升取正梯度方向，同样设置步长a；梯度下降选取负梯度方向，

线性回归:  假定服从高斯分布，通过MLE进行估计

logistics回归: 假定服从二项分布，通过MLE进行估计

如果都进行梯度下降法估计，会发现求解的方式都是一样的

广义线性模型的定义: 因变量不服从正态分布，且因变量与自变量不存在线性关系；广义就是要找一个非线性的关系f，使得转换后更接近因变量的分布

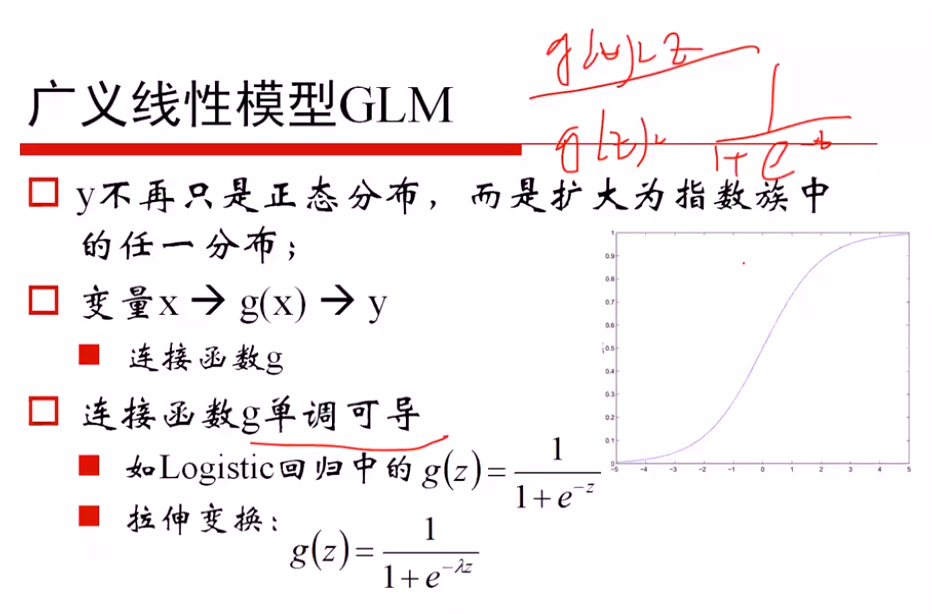
证明是一个广义的线性模型:

对数线性模型:

从对数模型理解 logistics函数

一方面: 从 ln(p/(1-p)) = θx 推导出 p = logistics函数，说明希望对数模型是线性的，从而推导出概率可以用logistics函数表示

另一方面: 从 p=logistics函数 + ln(p/(1-p))对数模型，推导出对数模型是线性的θTx

广义线性模型  → 相似的梯度下降方法

解法2: 从损失函数进行求解

(1)对 -1, 1转换为0, 1  进行(yi+1)/2...

softmax回归

鸢尾花数据

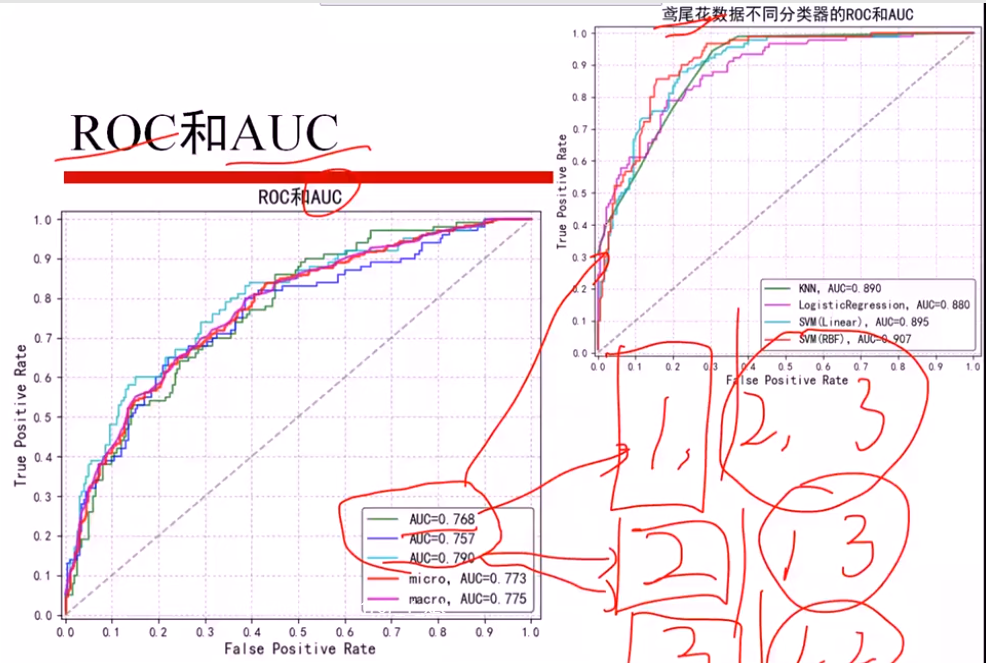
分为三个 二分类问题，算出三个AUCi值

micro: 直接算三个平均AUCi，得出AUC

macro: 总体加和，当作一个AUC计算