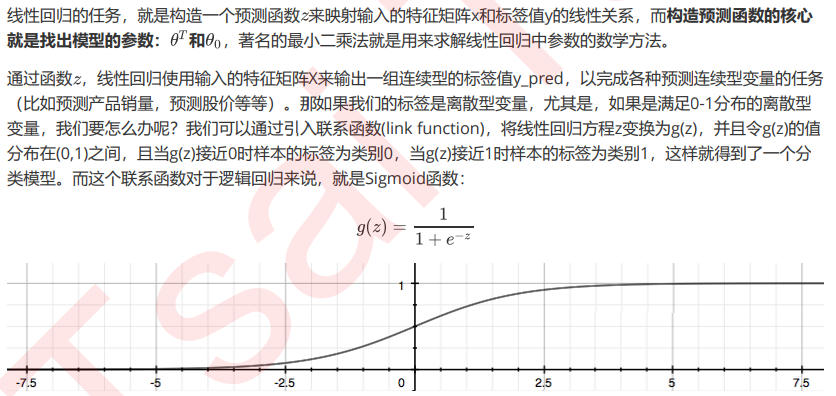
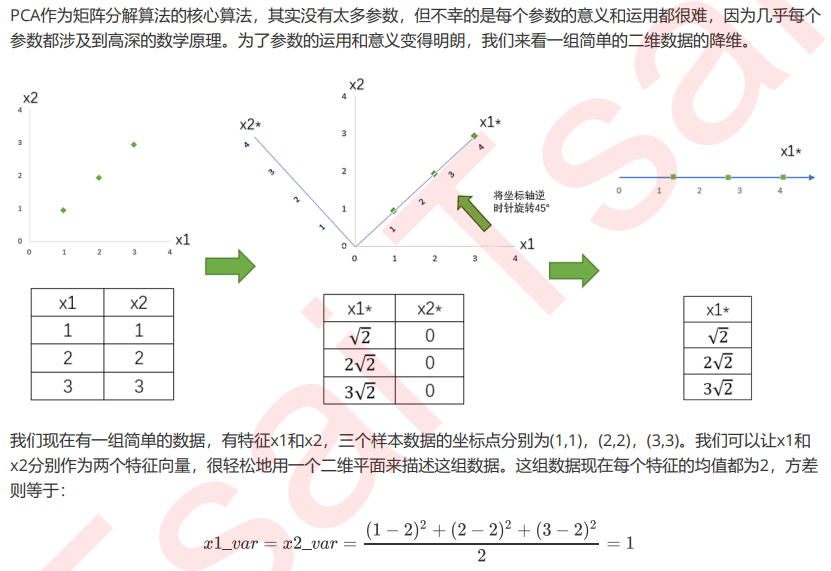
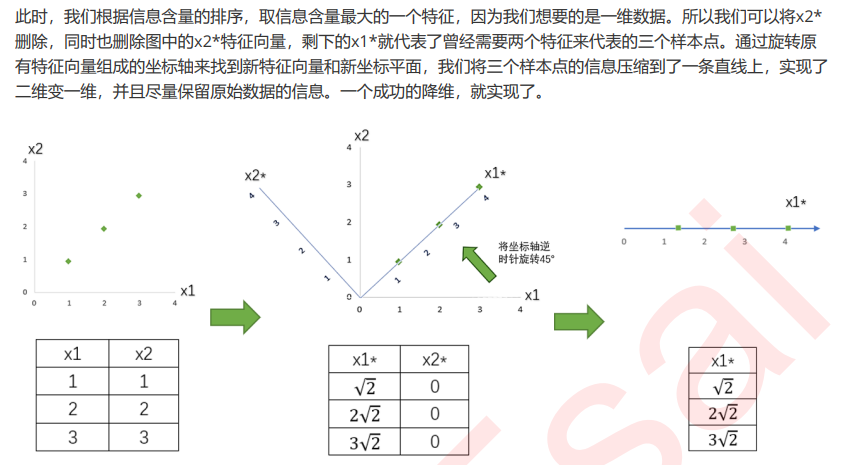
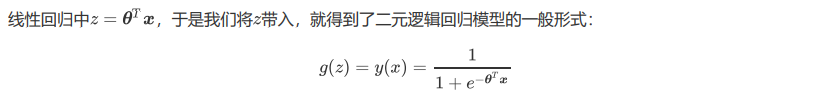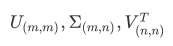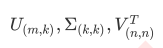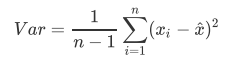支持向量机(SVM,也称为支持向量网络),是机器学习中获得关注最多的算法没有之一。它源于统计学习理论, 是我们除了集成算法之外,接触的第一个强学习器。它有多强呢?

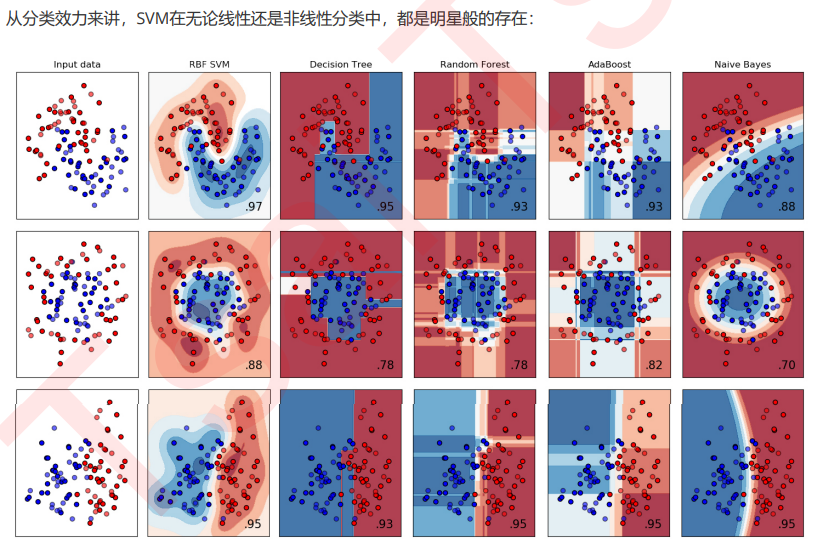
从实际应用来看,SVM在各种实际问题中都表现非常优秀。它在手写识别数字和人脸识别中应用广泛,在文本和超 文本的分类中举足轻重,因为SVM可以大量减少标准归纳(standard inductive)和转换设置(transductive settings)中对标记训练实例的需求。同时,SVM也被用来执行图像的分类,并用于图像分割系统。。除此之外,生物学和许多其他科学都是SVM的青睐者,SVM现在已经广泛被用于蛋白质分类,现 在化合物分类的业界平均水平可以达到90%以上的准确率。在生物科学的尖端研究中,人们还使用支持向量机来识 别用于模型预测的各种特征,以找出各种基因表现结果的影响因素。
从学术的角度来看,SVM是最接近深度学习的机器学习算法。线性SVM可以看成是神经网络的单个神经元(虽然损 失函数与神经网络不同),非线性的SVM则与两层的神经网络相当,非线性的SVM中如果添加多个核函数,则可以 模仿多层的神经网络。